Projects

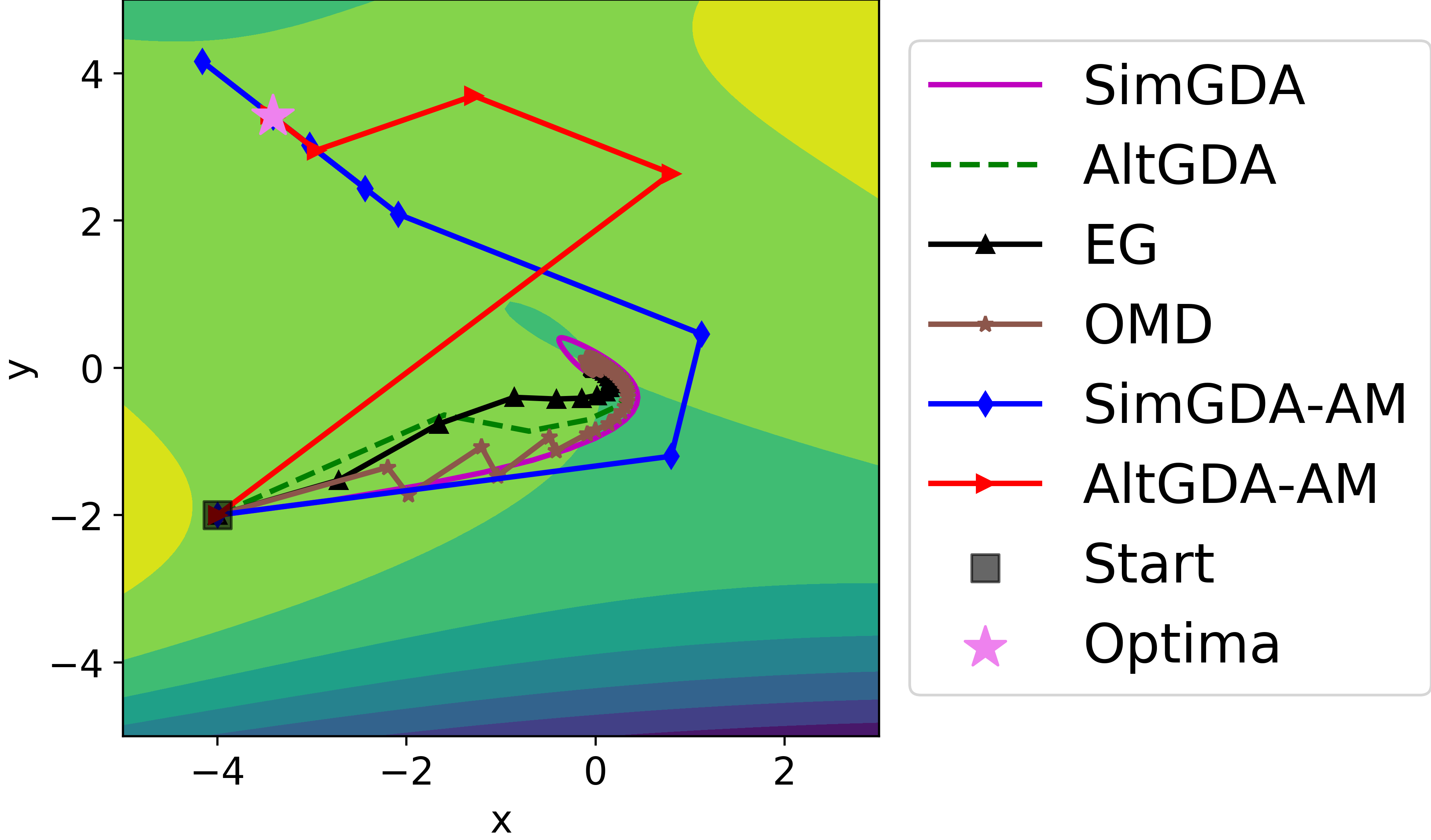Nonlinear Acceleration Methods in Data Science (Supported by NSF DMS 2208412)
In many disciplines of science and engineering one often encounters sequences of numbers or vectors or other mathematical objects. A common goal in these situations is to obtain the limit of the sequence inexpensively. One common solution is to transform the sequence, by ‘accelerating it’. This usually entails combining the terms of the sequence to produce new entries that reach the limit faster. So far, acceleration methods were developed by mathematicians and (quantum) physicists to deal with a wide range of problems from the physical sciences. The primary goal of this project is to study such acceleration methods and to adapt them to the modern era by focusing on topics related to machine learning and, more generally, data sciences.

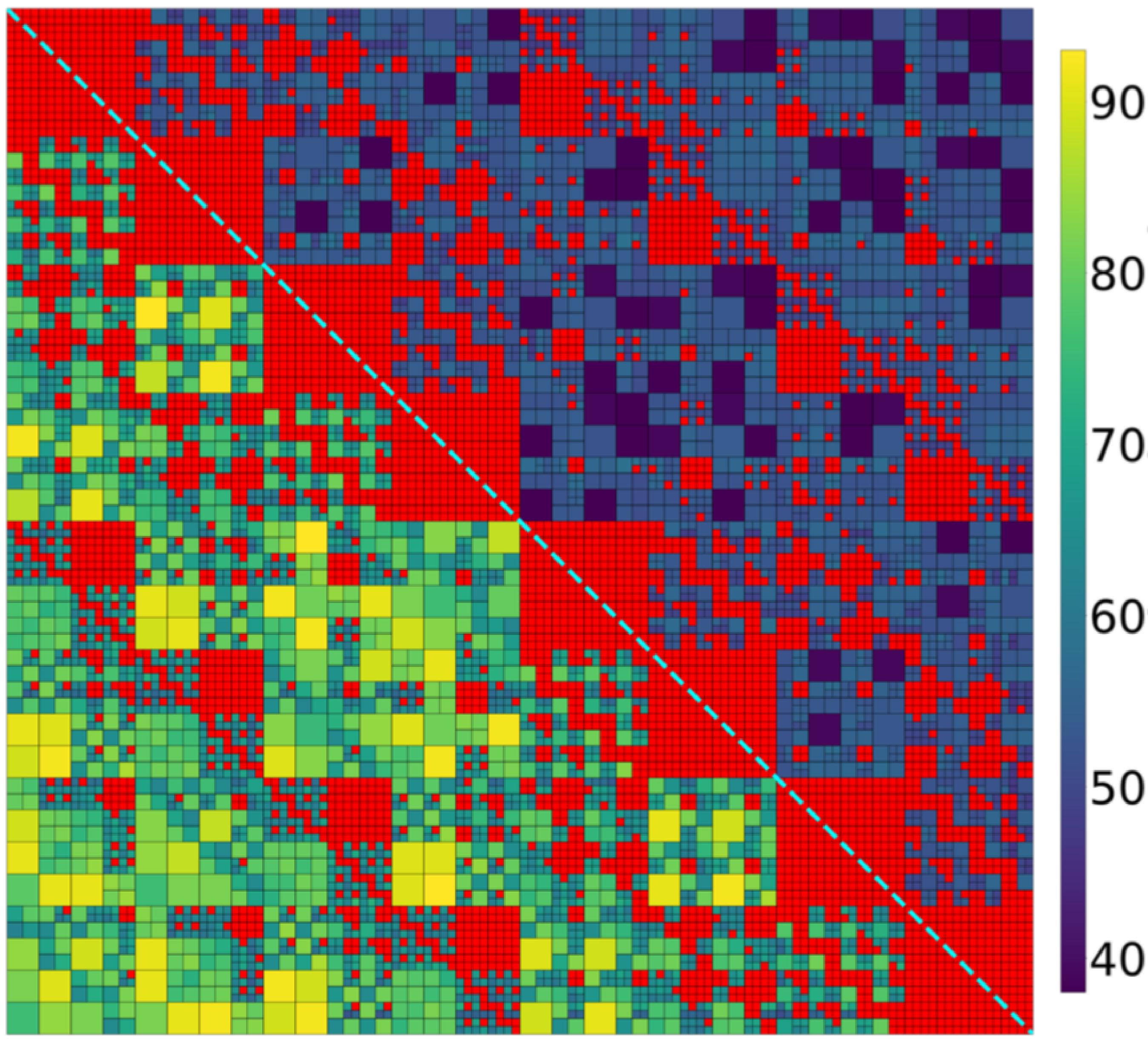Hierarchical Kernel Matrices for Scientific and Data Applications (Supported by NSF OAC 2003720)
This project specifically addresses high-dimensional problems, the use of specialized kernel functions in machine learning, and the high initial computational cost of constructing a hierarchical representation for a kernel matrix. New methods developed will be applied to large-scale cases in a scientific application and a machine learning application: Brownian dynamics and Gaussian process regression. In machine learning, the new methods will complement existing large-scale approaches for Gaussian processes. High-performance software will address specific scaling challenges in constructing hierarchical matrices.