Ongoing Research Projects
A Flexible Optimal Control Framework for Efficient Training of Deep Neural Networks

This project develops a new mathematical framework for deep learning based on the interpretation of certain deep neural networks as nonlinear time-dependent differential equations. This interpretation offers a new way to analyze the successes and failures of deep learning. Advances in deep learning will be made by adapting the wide array of tools available for related optimal control problems, including numerical optimization, partial and ordinary differential equations, inverse problems theory, and parallel processing, to the deep learning problem. Using these currently untapped resources provides rigorous new ways to design and train very deep neural networks that generalize well.
PI: Lars Ruthotto
Funding: US National Science Foundation CAREER award DMS 1751636
Novel methods for computational hemodynamics
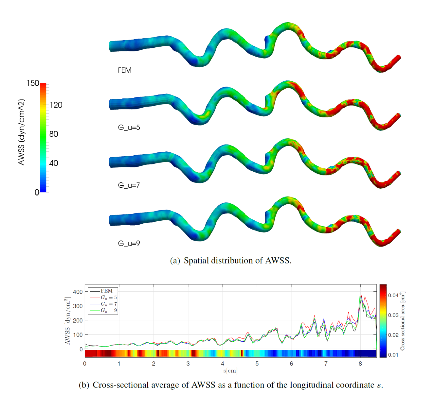
The incompressible Navier-Stokes equations are the basic mathematical model for the simulation of blood flow in arteries. Even if well-known and investigated since a long time, these equations still represent a numerical challenge for their saddle-point structure, the non linear nature. In medical applications, efficiency is a priority together with reliability. All these aspects require the set up of appropriate preconditioners, specific solution methods and, more in general, approaches that could take advantage from particular features of the problem at hand. In addition, we should consider (i) the presence of possible turbulent dynamics and their appropriate numerical modeling; (ii) the lack of data that systematically affects the clinical scenarios (defective problems, image legacy problem). The former is currently solved by Large Eddie Simulation (LES) approaches, specifically based on deconvolution filters. The latter calls for specific methods for the identification of the (arbitrary) missing conditions with low impact on the final solutions. Also, the presence of numerical instabilities induced by backflows is a critical issues in computational hemodynamics. Among the possible solution methods, we also include the Hierarchical Model Reduction technique, a numerical approach for incompressible flow in pipes, where finite elements or isogeometric analysis for the axial direction of the pipe are coupled with spectral methods for a rapid simulation of the transversal dynamics.
Funding: US National Science Foundation awards DMS 1419060 and DMS 1620406
This is joint work with Simona Perotto (Dept. Mathematics, Politecnico di Milano, Italy), Pablo Blanco (LNCC, Petropolis, Brazil), Annalisa Quaini (Dept. of Mathematics, University of Houston, TX), Leo Rebholz (Dept. of Mathematics, Clemson University, SC).
Efficient Algorithms for PDE-Parameter Estimation
This project develops efficient numerical methods for solving big data parameter estimation problems that involve partial differential equations (PDEs). Parameter estimation problems of this kind impose key challenges in many scientific disciplines, e.g., in medical imaging, geophysical imaging, and deep learning. The inverse problem can be formulated as an optimization problem with constraints that are given by the PDEs. The unknowns are parameters of the PDEs (e.g., physical properties of the object to be measured). The objective is to minimize the misfit between PDE simulations and measured data plus some regularization term.
The project aims at deriving efficient algorithms and massively parallel solvers for solving big data PDE parameter estimation problems. Its main thrusts are
- Reduced-order modeling techniques
- Stochastic optimization methods
- Parallel and distributed optimization problems
PI: Lars Ruthotto
Funding: US National Science Foundation award DMS 1522599
Algorithms for Inverse Problems that Exploit Kronecker Product and Tensor Structures
The aim of this project is to develop efficient singular value decomposition (SVD) approximation methods for large-scale matrices that arise in discrete ill-posed inverse problems. The approach will exploit inherent Kronecker product and tensor structures, and will be the basis for a computational platform for the efficient solution of large-scale ill-posed problems. Efficient approaches to solve Kronecker product and tensor structured SVD updating problems will be developed. Iterative methods that can incorporate regularization, sparse and low-rank constraints on the solution will also be considered. The SVD approximations and updating methods developed in this project can be used as tools to obtain approximate solutions of ill-posed inverse problems, as preconditioners to accelerate iterative solvers, or as tools to build solution methods for nonlinear problems. By developing a computational platform, based on SVD approximations, the work developed in this proposal will have a broad scientific impact for applications where it is necessary to compute solutions of large-scale ill-posed inverse problems, including astronomy, cosmology, geophysics, microscopy, and medical imaging.
PI: James Nagy
Funding: US National Science Foundation award DMS 1522760
Data Assimilation and Parameter identification in electrophysiology
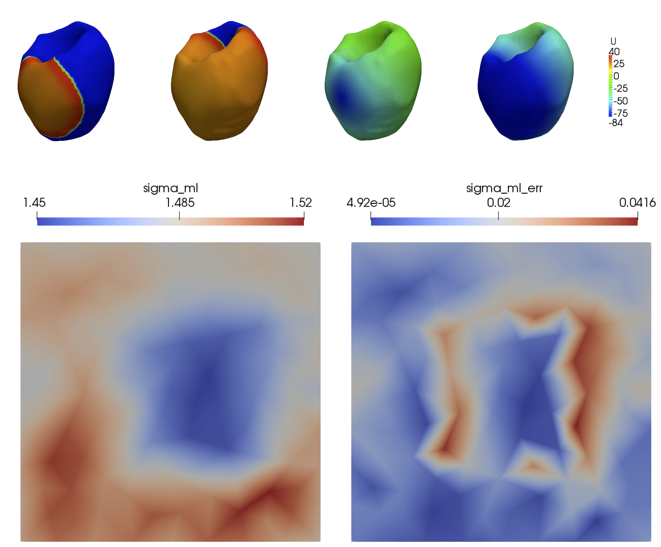
Data Assimilation is the ensemble of methods for merging data and numerical simulations when solving a specific problem. It can be pursued in different ways and for addressing different problems, from prediction to parameter identification. In this project, we specifically address the variational estimation of the conductivity parameters of the Bidomain equations. These are partial differential equations for the potential propagation in the cardiac tissue. The conductivity tensor is a critical set pf parameters with a major impact on the numerical solution. Their accurate knowledge is hard to obtain in practice. Moving from measurements of the potential on the surface of the tissue, it is possible to obtain a reliable estimate to be used in more complex problems like the optimal placement of cardiac leads. We pursue a variational approach, i.e. the minimization of the mismatch between data and simulations, constrained by the Bidomain equations or their simplified version, the Mondomain equation. As the computational costs are quite high, we need reduced models to pursue the estimation in short timelines. We work currently with approaches like Proper Orthogonal Decomposition and Proper General Decomposition.
Funding: US National Science Foundation award DMS 1412963
This is joint work with F. Fenton (Dept. of Physics, GA Tech), A. Gizzi (Campus Biomedico, Rome, IT), S. Perotto (Dept. of Mathematics, Politecnico di Milano, IT).
Numerical Methods for Multispectral Tomographic Image Reconstruction
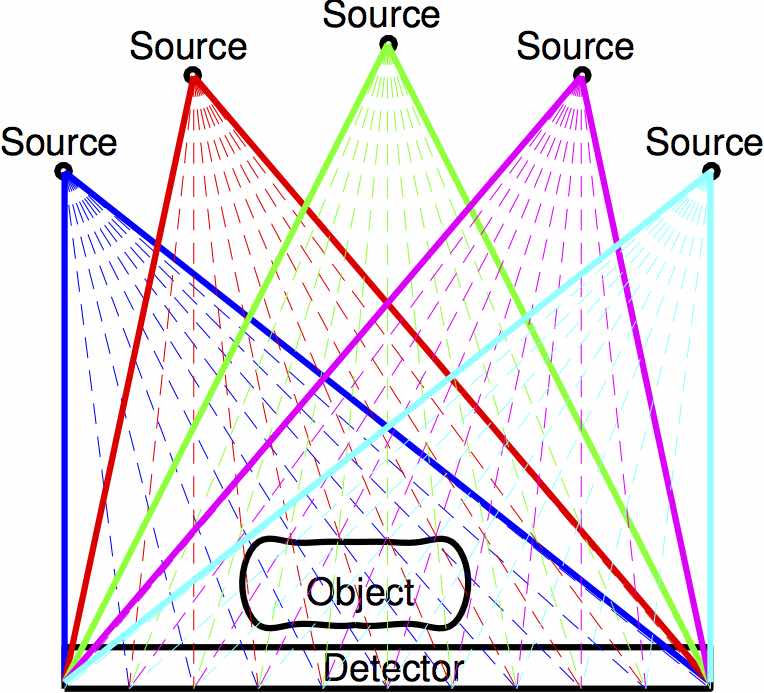
Breast cancer is the most prevalent non-skin cancer in women in the US. Although mammography is currently the most common test for the early detection and diagnosis of breast cancer, its two-dimensional nature introduces various limitations in its capabilities for advanced imaging. Over the last decade, the introduction of digital imaging technology has resulted in the development of new tomographic and pseudo-tomographic methods for imaging the breast.
Digital tomographic image reconstruction uses multiple x-ray projections obtained along a range of different incident angles to reconstruct a 3D representation of an object. For example, computed tomography (CT) generally refers to the situation when a full set of angles are used (e.g., 360 degrees) while tomosynthesis refers to the case when only a limited (e.g., 30 degrees) angular range is used. In either case, most existing reconstruction algorithms assume that the x-ray source is monoenergetic. This results in a simplified linear forward model, which is easy to solve but can result in artifacts in the reconstructed images. It has been shown that these artifacts can be reduced by using a more accurate polyenergetic assumption for the x-ray source, but the polyenergetic model requires solving a large-scale nonlinear inverse problem. In addition to reducing artifacts, a full polyenergetic model can be used to extract additional information about the materials of the object; that is, to provide a mechanism for quantitative imaging. Similar mathematical models arise when using multispectral detectors.
The aim of this project is to develop algorithms and software to solve these very challenging inverse problems.
PI: James Nagy
This is joint work with Martin Andersen, Technical University of Denmark, and Ioannis Sechopoulos, Radboud University Medical Center, and is paritally funded by a grant from the US National Institute of Health.
Bayesian Approaches for Strain Identification from Culture-Independent Samples
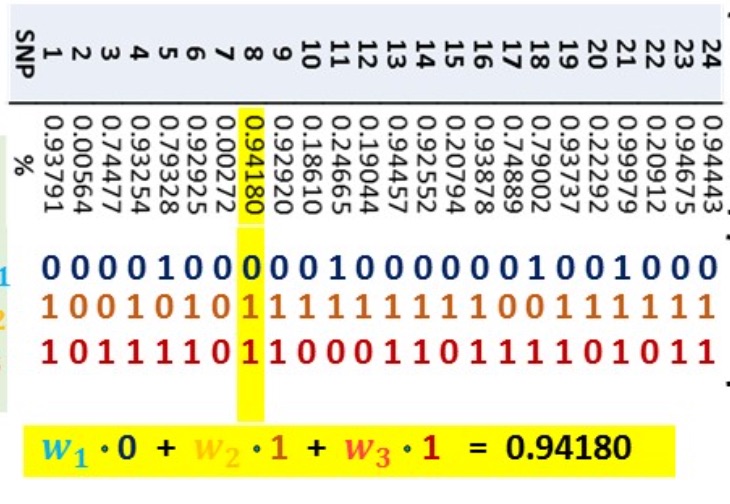
We develop new mathematical approaches, algorithms and systems for identifying pathogen strains using whole genome multilocus sequence typing (wgMLST) data in mixed samples. Strain identification is an underdetermined inverse problem when the samples are not cultured, i.e., contain multiple strains at unknown proportions. Therefore, we encode prior knowledge on both the strains and their proportion in a Bayesian framework. Our approaches use mixed-integer optimization to identify the most likely strains and Monte-Carlo sampling to quantify the uncertainty associated with those estimates. Motivating applications of our algorithms include the identification of P. falciparum (malaria) and E.coli (foodborne illness) strains to improve visibility and monitoring for public health officials.
PIs: Lars Ruthotto, Ymir Vigfusson, and Rebecca Mitchell