MATH 111 Calculus I \(\quad\;\;\) Instructor: Difeng Cai

2.1 The Tangent and Velocity Problems

The worksheet (with solutions) can be found here

Equation of a Line

• The point-slope form of a line through \((x_1,y_1)\) with slope \(m\) is \[y-y_1=m(x-x_1)\]
• The two-point form of a line through two points \((x_1,y_1)\), \((x_2,y_2)\) is \[y-y_1=\frac{y_1-y_2}{x_1-x_2}(x-x_1)\]

Ex. Find the slope of the line through \((0,1)\) and \((5,4)\).

Ex. Find the equation of the line through \((1,1)\), \((0,-2)\) and sketch its graph.

Ex. What is the equation of the line that passes through \((1,0)\) and is parallel to the line passing through \((0,1)\) and \((5,4)\)? (Hint: find the slope first.)

Secant Line and Tangent Line

A secant line is a line that cuts a curve more than once.
A tangent line is a line that touches the curve, having the same direction as the curve at the point of contact.

The slope of the tangent line is the limit of the slopes of the secant lines (when one intersection moves to the point of contact).

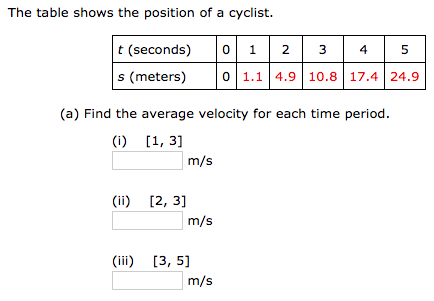
Average Velocity and Instantaneous Velocity

• 'Average velocity' = \(\frac{\text{distance traveled}}{\text{time elapsed}}\), corresponding to slope of secant line in distance-time plot.
• 'Instantaneous velocity at \(t\)' = limit of average velocity over shorter and shorter time periods that start at moment \(t\), corresponding to slope of tangent line in distance-time plot.