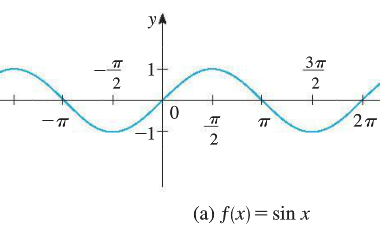
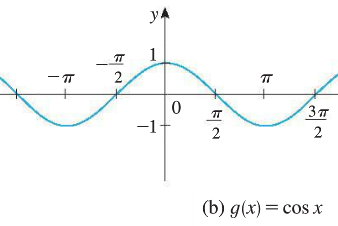
Convention in calculus: radian measure is used (unless otherwise indicated). That is, use \(\pi/2\) instead of \(90^{\circ}\).
A review on unit circle can be found here
For both sine and cosine functions, domain: \((-\infty,\infty)\); range: \([-1,1]\). \[-1\leq \sin x \leq 1\quad\quad -1\leq \cos x \leq 1\]
Periodic with a period of \(2\pi\): \[\sin(x+2\pi)=\sin x\quad\quad \cos(x+2\pi)=\cos x\]
Values at certain points: \[\sin 0 =0, \;\; \sin \frac{\pi}{6} = \frac{1}{2},\;\; \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2},\;\; \sin \frac{\pi}{3} = \frac{\sqrt{3}}{2},\;\;\sin\frac{\pi}{2}=1,\;\; \sin \frac{2\pi}{3}=\frac{\sqrt{3}}{2}\] \[\cos 0 =1, \;\; \cos \frac{\pi}{6} = \frac{\sqrt{3}}{2},\;\; \cos \frac{\pi}{4} = \frac{\sqrt{2}}{2},\;\; \cos \frac{\pi}{3} = \frac{1}{2},\;\; \cos \frac{\pi}{2} =0,\;\;\cos \frac{2\pi}{3}=-\frac{1}{2}\]
Symmetry: \(y=\sin x\) is an odd function, \(y=\cos x\) is an even function \[\sin (-x) = -\sin x\] \[\cos(-x)=\cos x\]
Zeros: \[ \begin{aligned} \sin x &= 0\quad \text{when}\;\; x=n\pi \;\;\text{for any integer}\; n\\ \cos x &= 0\quad\text{when}\;\; x=\frac{\pi}{2}+n\pi\;\;\text{for any integer}\; n \end{aligned} \]


Tangent function:
\[\tan x = \frac{\sin x}{\cos x}\]
Domain: \(x\neq \pi/2+n\pi\) for all integer \(n\);
range: \((-\infty,\infty)\)
Periodic with period = \(\pi\):
\[\tan (x+\pi) = \tan x\]
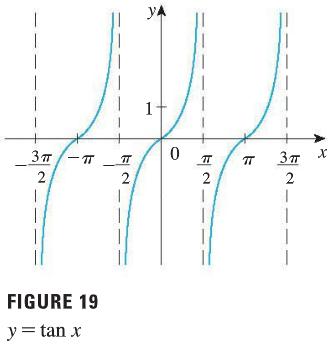
See "Appendix D" in the textbook for cosecant(csc), secant(sec), cotangent(cot) functions (who are reciprocals of sine, cosine, tangent).