Section 3.1
Taylor Polynomials
Goals:
1 Approximate a function with a Taylor polynomial.
2 Compute error bounds for a Taylor polynomial.
Question 3.1.1
How Can We Improve on a Linearization?
Formula
The linearization or tangent line to a function f (x) at a has the
equation.
L(x) = f (a) + f
′
(a)(x − a)
By design f and L have
1 Equal values at a.
2 Equal first derivatives at a.
We could make a better approximation, if we could match second, third,
fourth derivatives of f (x). A line cannot do that, but a polynomial can.
165
Question 3.1.2
What Is a Taylor Polynomial?
Definition
The n
th
Taylor polynomial of f (x) at x = a is a degree n polynomial
that shares the value and first n derivatives of f at x = a. Its formula is
T
n
(x) =
n
X
k=0
f
(k)
(a)
k!
(x − a)
k
.
Remarks
The variable is x. f
(k)
(a) is not a function but a number.
f
(0)
is the zeroth derivative, meaning f
(0)
(a) = f (a).
0! is defined to be 1.
166
Example 3.1.3
Computing a Taylor Polynomial
a Find the degree 3 Taylor polynomial of y =
√
x at x = 4.
b Use it to estimate
√
5.
167
Example 3.1.4
Writing a Sum in Σ Notation
Write each of the following sums in Σ notation.
a 4 + 7 + 10 + 13 + 16 + 19 + 22
b 2 + 6 + 18 + 54 + 162 + 486
c −3 + 4 − 5 + 6 −7 + 8 − 9 + 10
d
1
4
+
√
2
9
+
√
3
16
+
2
25
+
√
5
36
168
Example 3.1.5
A Taylor Polynomial in
P
Notation
Write the 10th degree Taylor Polynomial for f (x) =
1
x
2
centered at x = 3.
169
Question 3.1.6
How Accurate Is the Taylor Polynomial?
Theorem
Let f and g be differentiable functions. Consider an interval [a, b], and
suppose f (a) = g (a).
1 If f
′
(x) = g
′
(x) on [a, b], then f (x) = g(x) on [a, b]
2 If f
′
(x) < g
′
(x) on [a, b], then f (x) < g(x) on (a, b]
Reasoning
Intuitive If two functions start at the same value at a, then the one
that grows faster will have a higher value at b.
Formal The Fundamental Theorem of Calculus says
f (x) − f (a) =
Z
x
a
f
′
(t)dt g(x) − g(a) =
Z
x
a
g
′
(t)dt.
Larger functions have larger integrals.
170
Question 3.1.6
How Accurate Is the Taylor Polynomial?
Figure: Two functions with a common value at a: f (x) with a smaller derivative
and g(x) with a larger derivative.
171
Question 3.1.6
How Accurate Is the Taylor Polynomial?
Notation
Given a function f (x) and its nth Taylor polynomial T
n
(x) centered at a,
the remainder at x is
R
n
(x) = f (x) − T
n
(x)
If we are using T
n
(x) to approximate f (x),
R
n
(x) = −error of T
n
(x).
We should be very interested in knowing the value of R
n
(x). We will use
our derivative comparison theorem to make two arguments
1 If f
(n+1)
(x) is a constant M, then we can compute R
n
(x) exactly.
2 If |f
(n+1)
(x)| ≤ M then the error in 1 is the worst-case scenario.
172
Question 3.1.6
How Accurate Is the Taylor Polynomial?
Theorem
If f
(n+1)
(x) is a constant M on [a, b], then
f (x) = T
n+1
(x) = T
n
(x) +
M
(n + 1)!
(x − a)
n+1
.
d
dx
n+1
f (x) =
d
dx
n+1
T
n+1
(x) = M on [a, b]
d
dx
n
f (a) =
d
dx
n
T
n+1
(a)
d
dx
n
f (x) =
d
dx
n
T
n+1
(x) on [a, b]
d
dx
n−1
f (a) =
d
dx
n−1
T
n+1
(a)
d
dx
n−1
f (x) =
d
dx
n−1
T
n+1
(x) on [a, b]
d
dx
f (a) =
d
dx
T
n+1
(a)
d
dx
f (x) =
d
dx
T
n+1
(x) on [a, b]
f (a) = T
n+1
(a) f (x) = T
n+1
(x) on [a, b]
Because derivatives and values of
a Taylor polynomial match the function
173
Question 3.1.6
How Accurate Is the Taylor Polynomial?
But what if f
(n+1)
(x) is not a constant? In this case we will settle for a
bound on f
(n+1)
(x).
Theorem (Taylor’s Inequality)
If
f
(n+1)
(t)
≤ M for all x between a and b, then for all x between a
and b,
|R
n
(x)| ≤
M
(n + 1)!
(x − a)
n+1
174
Question 3.1.6
How Accurate Is the Taylor Polynomial?
To prove Taylor’s Inequality, we compare the derivatives of f (x) with the
worst-case scenario w(x) = T
n
(x) +
M
(n+1)!
(x − a)
n+1
.
d
dx
n+1
f (x) ≤
d
dx
n+1
w(a) = M on [a, b]
d
dx
n
f (a) =
d
dx
n
w(a)
d
dx
n
f (x) ≤
d
dx
n
w(x ) on [a, b]
d
dx
n−1
f (a) =
d
dx
n−1
w(a)
d
dx
n−1
f (x) ≤
d
dx
n−1
w(x ) on [a, b]
d
dx
f (a) =
d
dx
w(a)
d
dx
f (x) ≤
d
dx
w(x ) on [a, b]
f (a) = w(a) f (x) ≤ w(x) on [a, b]
Because M is a bound on
d
dx
n+1
f (x)
Because derivatives and values of
a Taylor polynomial match the function
175
Question 3.1.6
How Accurate Is the Taylor Polynomial?
To finish the argument we need to
1 Produce a lower bound for f using w(x) = T
n
(x) −
M
(n+1)!
(x −a)
n+1
.
2 Solve the inequality bounds for R
n
(x).
T
n
(x) −
M
(n + 1)!
(x − a)
n+1
≤ f (x) ≤ T
n
(x) +
M
(n + 1)!
(x − a)
n+1
−
M
(n + 1)!
(x − a)
n+1
≤ R
n
(x) ≤
M
(n + 1)!
(x − a)
n+1
3 Repeat for intervals of the form [b, a]. These work the same way
with a sign reversed.
176
Example 3.1.7
A Taylor Approximation Error Bound
Let f (x) = sin x.
a Give a general form for the n
th
Taylor polynomial for f at x = 0.
b Find a bound on f
(n)
(x) for each n.
c What happens to the error bound as x increases but n stays the
same?
d What happens to the error bound as n increases but x stays the
same?
e What does this tell us about the relationship between the T
n
(x)
approximations and f (x)?
177
Example 3.1.7
A Taylor Approximation Error Bound
Let f (x) = sin x.
a Give a general form for the n
th
Taylor polynomial for f at x = 0.
177
Example 3.1.7
A Taylor Approximation Error Bound
Let f (x) = sin x.
b Find a bound on f
(n)
(x) for each n.
177
Example 3.1.7
A Taylor Approximation Error Bound
Let f (x) = sin x.
c What happens to the error bound as x increases but n stays the
same?
177
Example 3.1.7
A Taylor Approximation Error Bound
Let f (x) = sin x.
d What happens to the error bound as n increases but x stays the
same?
177
Example 3.1.7
A Taylor Approximation Error Bound
Let f (x) = sin x.
e What does this tell us about the relationship between the T
n
(x)
approximations and f (x)?
177
Example 3.1.7
A Taylor Approximation Error Bound
Figure: f (x) = sin x approximated by its Taylor polynomials, T
n
(x)
178
Example 3.1.7
A Taylor Approximation Error Bound
Main Ideas
In order to understand how the error changes as n increases, we
need to have an expression for f
(n)
(x).
We can choose M to be the largest value of |f
(n+1)
| on the interval
[a, x]. This may not be the value of |f
(n+1)
(a)|.
In general, Taylor polynomials will become less accurate the farther
you get from a.
We can often mitigate this inaccuracy by choosing larger values of n.
179
Example 3.1.7
A Taylor Approximation Error Bound
Some functions are not well estimated by their Taylor polynomial.
Example
f (x) =
(
0 if x ≤ 0
e
−
1
x
if x > 0
f
(k)
(0) = 0 for all k. So the
Taylor polynomial at x = 0 is
T
n
(x) =
n
X
k=0
0x
k
.
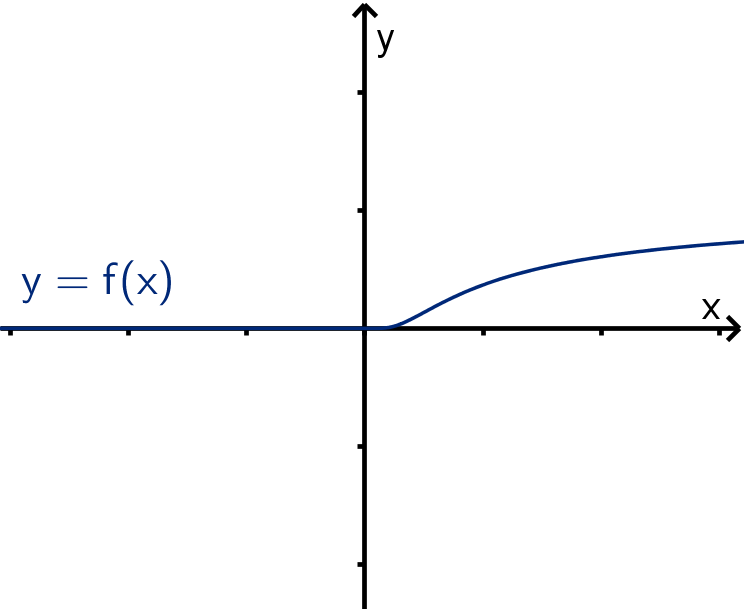
No matter how large n gets, T
n
(x) will not get any closer to f (x) for any
x > 0.
180
Example 3.1.7
A Taylor Approximation Error Bound
How can this happen, given Taylor’s Inequality? The derivatives of f get
bigger and bigger. M grows so fast that the error R
n
(x) gets no smaller.
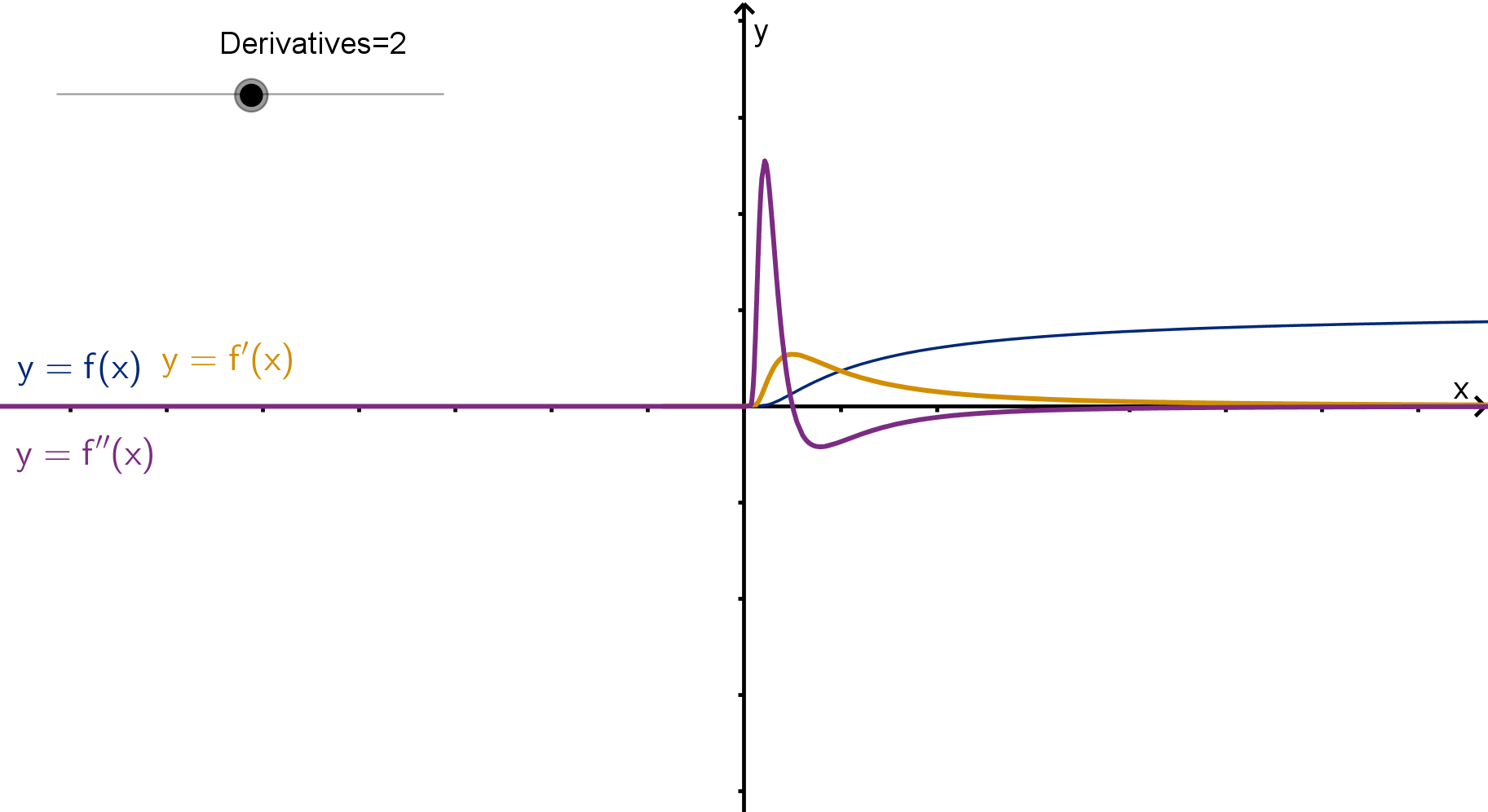
Figure: A function whose derivative bounds grow factorially
181
Section 3.1
Summary Questions
Q1 Why do we use Taylor polynomials?
Q2 Why is there a denominator of k! in the formula for a Taylor
polynomial?
Q3 Explain why we’d always rather center a Taylor polynomial for
y = ln x at x = 1.
Q4 What properties make a Taylor polynomial T
n
(x) a better
approximation of f (x)?
182
Section 3.1
Q6
Suppose you were locked in a room with only a pencil and paper and
asked to compute the first ten decimal places of the following numbers:
4
17
√
7 e
Which could you compute?
For the ones you can compute, how would you do it?
183
Section 3.1
Q28
Let f (x) = xe
x
.
a Compute the Taylor polynomial T
3
(x) for f (x) centered at x = 0.
b Compute the theoretical error bound for T
3
(2).
c Explain the difficulties that would arise from this error bound, if your
goal is to approximate f (2) by hand. Can you resolve them?
184
Section 3.1
Q30
Consider the graph of y = f (x) below.
a Suppose you wanted to produce the second degree Taylor
polynomial of f centered at a = −1. Indicate whether the constant
term and each coefficient would be positive or negative. Provide
evidence for your answer.
b Would T
2
(4) underestimate or overestimate f (4)? Explain.
185
Section 3.2
Sequences
Goals:
1 Use notation to describe the terms of an infinite sequence.
2 Calculate the limit of an infinite sequence.
Question 3.2.1
What Is a Sequence?
A sequence is an ordered set of numbers. If this set is infinite, we can
most rigorously define it by giving a general formula for the n
th
term for
some index variable n. Here are three different notations for the same
sequence.
1
2
,
2
3
,
3
4
,
4
5
. . .
n
n + 1
∞
n=1
a
n
=
n
n + 1
187
Question 3.2.2
What Is the Limit of a Sequence?
Definition
If we can make the elements of a sequence a
n
arbitrarily close to some
number L by considering only n above a certain number, then we write
lim
n→∞
a
n
= L
and we say the sequence converges to L. If a
n
does not converge to any
such L then we say it diverges.
188
Question 3.2.2
What Is the Limit of a Sequence?
Remarks
The first few or even the first thousand terms of a sequence have no
bearing on the limit. We only care that we can eventually get close
to L.
“Arbitrarily close” means any level of closeness than anyone could
ask for. Eventually the sequence must be within
1
100
of L, and
1
1000
and
1
1000000
.
189
Question 3.2.2
What Is the Limit of a Sequence?
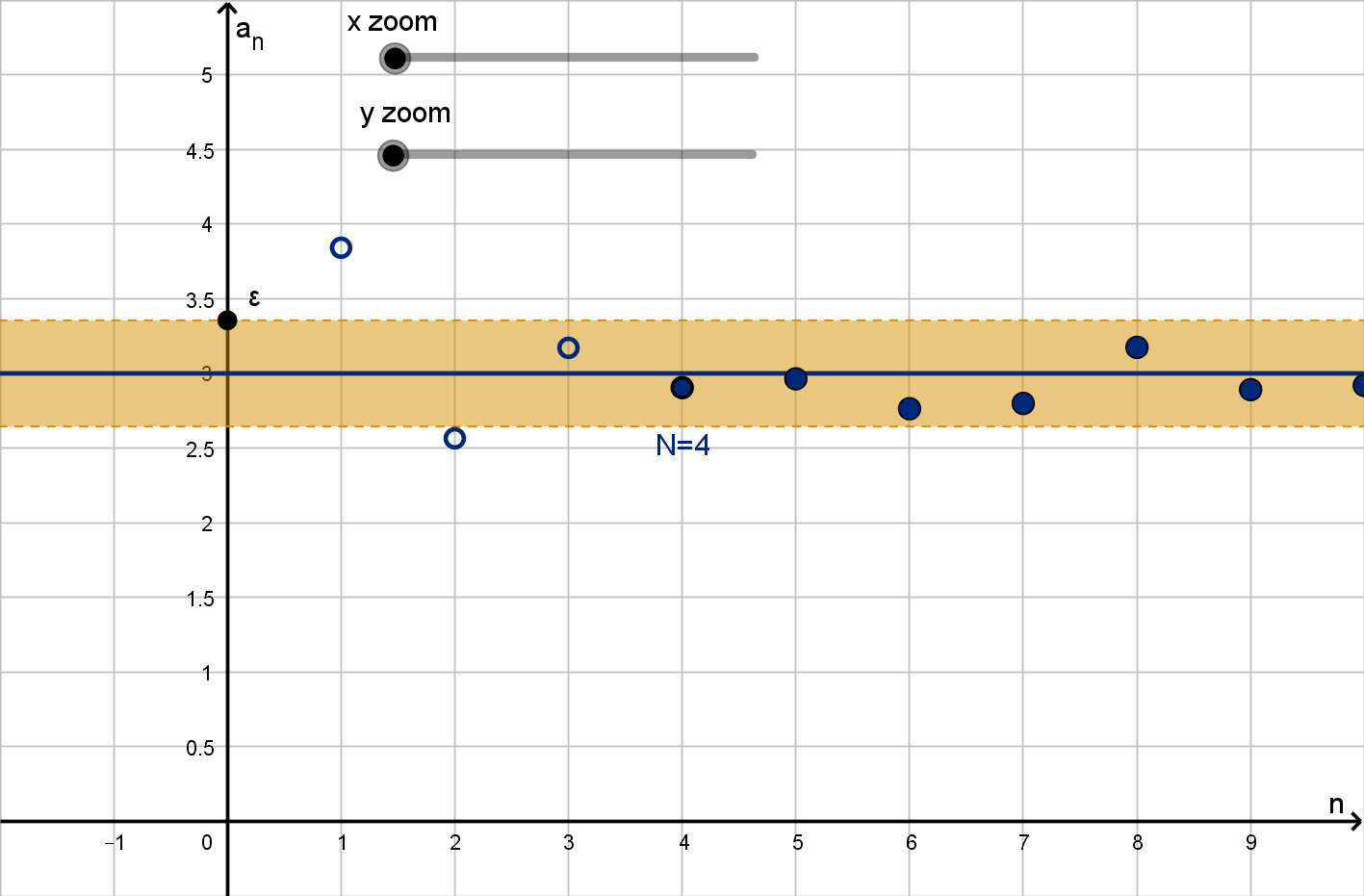
Figure: A sequence converging to L = 3
190
Example 3.2.3
Computing a Limit
Calculate lim
n→∞
n
n + 1
191
Example 3.2.3
Computing a Limit
Calculate lim
n→∞
n
n + 1
1
2
,
2
3
,
3
4
,
4
5
. . .
191
Example 3.2.3
Computing a Limit
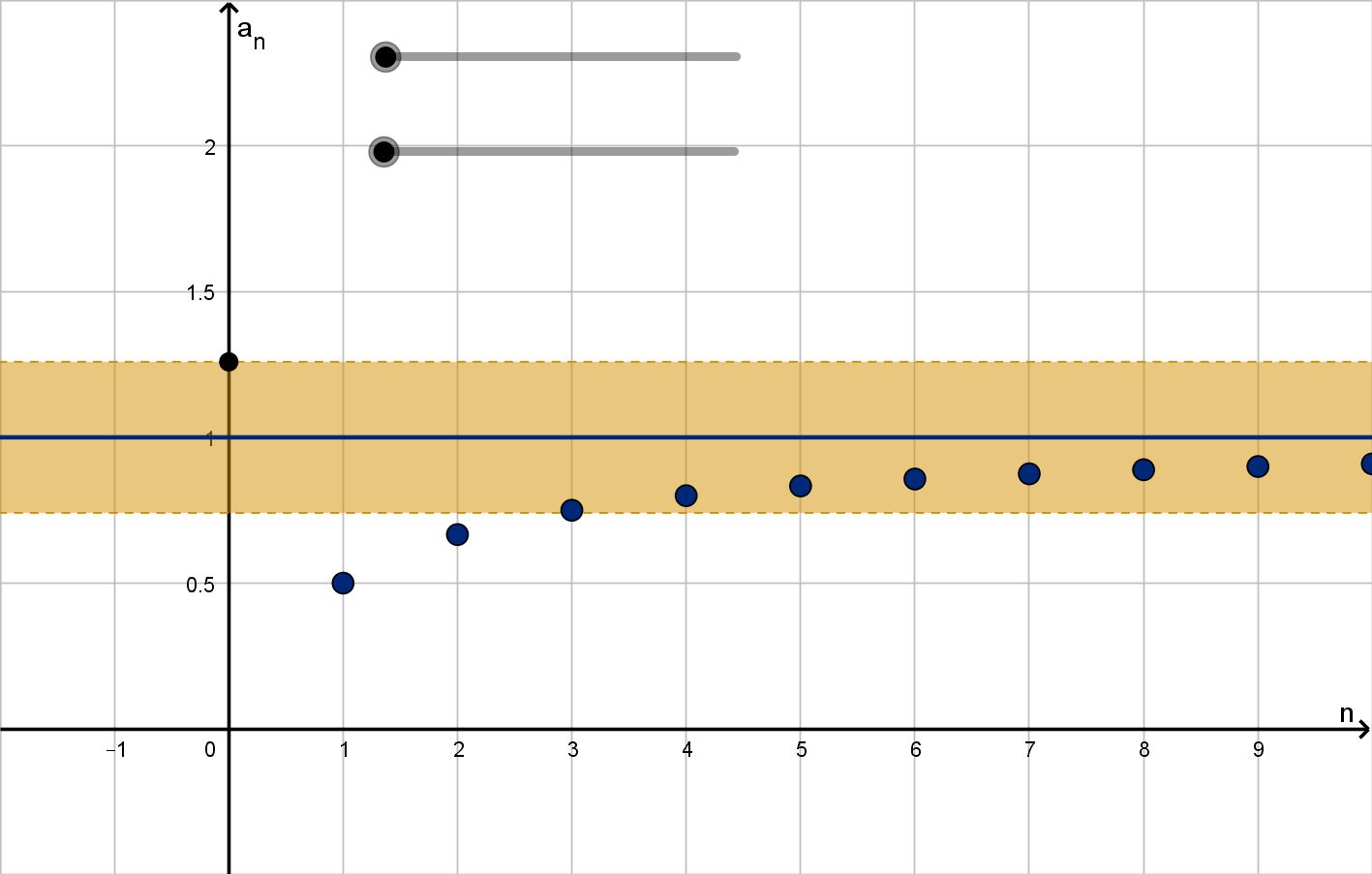
Figure: The sequence
n
n+1
converges to L = 1.
192
Question 3.2.4
How Are Limits of Sequences and Functions Related?
Theorem
Suppose for a sequence a
n
, there is a function f (x) such that f (n) = a
n
for all n (or at least all n sufficiently large). If
lim
x→∞
f (x) = L
we can conclude that
lim
n→∞
a
n
= L.
193
Example 3.2.5
Sequence Limits Using Functions
Find limits of the following sequences:
a lim
n→∞
2n
n + 3
b lim
n→∞
1
n
3
c lim
n→∞
e
−n
d lim
n→∞
n
2
e
n
e lim
n→∞
(−1)
n
194
Example 3.2.5
Sequence Limits Using Functions
Theorems
All of the laws for limits of functions at infinity also apply to limits of
sequences. For instance suppose lim
n→∞
a
n
= L and lim
n→∞
b
n
= M. If
c
n
= a
n
+ b
n
then
lim
n→∞
c
n
= L + M.
195
Synthesis 3.2.6
Indeterminate Forms with Factorials
Dominance
We say f (x) dominates g(x) if lim
x→∞
f (x)
g(x)
= ±∞. We write
f (x) >> g (x)
Even if you include a constant multiple or add multiple functions
together, the dominant function will outgrow any combination of
dominated ones. We have already established an order of dominance
using l’Hˆopital’s rule:
exponential
(larger base>>smaller base)
>>
polynomial
(larger degree>>smaller)
>>
root
(smaller power>>larger)
>>
logarithm
(smaller base>>larger)
196
Synthesis 3.2.6
Indeterminate Forms with Factorials
Theorem
As n → ∞, n! will eventually dominate any exponential function (and
thus any polynomial, root or logarithm).
197
Section 3.2
Summary Questions
Q1 Why do we use n instead of x as an index for a sequence?
Q2 Describe three different ways of denoting a sequence.
Q3 When is the limit of a sequence equal to the limit of a function?
Q4 If a
n
= b
n
+ 1000 for 1 ≤ n ≤ 2000000, what does that tell us about
the limits lim
n→∞
a
n
and lim
n→∞
b
n
?
198
Section 3.2
Q12
Consider the sequence a
n
= n sin(πn)
a What is lim
x→∞
x sin(πx)?
b Compute the first few values a
1
, a
2
, a
3
, and a
4
.
c What is lim
n→∞
n sin(πn)?
d Does this contradict one of our theorems? Explain.
199
Section 3.2
Q12
Remark
Read theorems carefully. The hypothesis and conclusion are not
interchangeable. Mixing them up can turn a true theorem into a false
one.
199
Section 3.2
Q24
Let T
n
(x) be the nth Taylor polynomial of f (x) = ln x centered at x = 1.
a Write an expression for T
n
(x) using Σ notation.
b Write an expression for the error bound of T
n
(x) for some x
between 0 and 1.
c For what values of x will the error bound shrink to 0 as n goes to
∞?
200
Section 3.2
Q24
a Write an expression for T
n
(x) using Σ notation.
200
Section 3.2
Q24
b Write an expression for the error bound of T
n
(x) for some x
between 0 and 1.
200
Section 3.2
Q24
c For what values of x will the error bound shrink to 0 as n goes to
∞?
200
Section 3.3
Series
Goals:
1 Identify partial sums of a series.
2 Recognize harmonic and alternating harmonic series.
3 Apply the divergence test.
4 Evaluate geometric series.
5 Apply the ratio test.
Question 3.3.1
What Is a Series?
You have been encountering series since you first learned about decimals.
You likely have not seen a rigorous description of what they mean.
0.33333333 . . . 3.1415926...
We can write
0.3333 . . . =
3
10
+
3
100
+
3
1000
+
3
10000
+ ···
or
3.1415 . . . = 3 +
1
10
+
4
100
+
1
1000
+
5
10000
+ ···
You may have an intuitive sense of what these quantities are, but what
does it mean to add up infinitely many numbers?
202
Question 3.3.1
What Is a Series?
Definition
A series is a sum of the form
∞
X
k=1
a
k
where a
k
is an infinite sequence. If
it is more convenient, we can give k a different initial value. If the
context is clear, we can write
X
a
k
as a shorthand.
Example
0.33333 . . . =
∞
X
k=1
3
10
k
The harmonic series is
∞
X
k=1
1
k
This tells us what a series is but not how to evaluate it. How do we
know that, for example
0.333 . . . =
1
3
?
203
Question 3.3.1
What Is a Series?
We evaluate a series by associating it with a sequence of partial sums.
Definition
The n
th
partial sum of the series
∞
X
k=1
a
k
is
s
n
= a
1
+ a
2
+ a
3
+ ···+ a
n
A series
∞
X
k=1
a
k
converges to L if
lim
n→∞
s
n
= L.
A series that does not converge to any L diverges.
Vocabulary Note
Do not confuse a sequence with a series. One is a list of numbers. The
other is the sum of a list of numbers.
204
Example 3.3.2
Computing Partial Sums
Consider
∞
X
k=1
3
10
k
.
a Compute the first few partial sums s
1
, s
2
, s
3
of this series.
b Compute lim
n→∞
s
n
205
Example 3.3.2
Computing Partial Sums
Main Idea
Often, we can show that
∞
X
k=1
a
k
= L by computing L − s
n
and seeing that
it converges to 0.
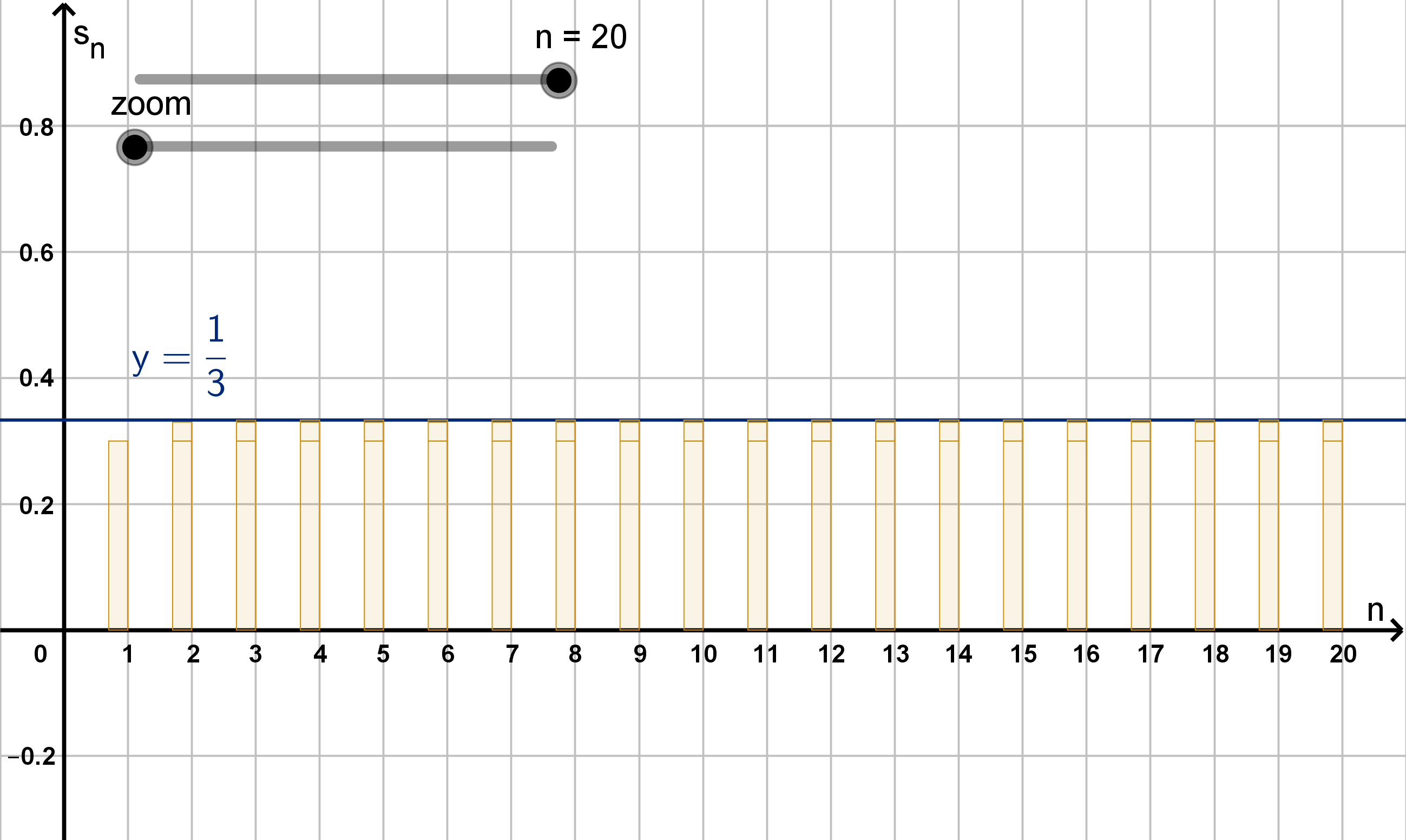
Figure: The partial sums s
n
converging to L =
1
3
206
Example 3.3.3
The Harmonic Series
Consider a partial sum of the harmonic series
∞
X
k=1
1
k
.
s
8
=
1
1
+
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
1
7
+
1
8
>
1
1
+
1
2
+
1
4
+
1
4
| {z }
1
2
+
1
8
+
1
8
+
1
8
+
1
8
| {z }
1
2
=1 +
1
2
+
1
2
+
1
2
In general we can make s
n
bigger than any integer c by setting n = 2
m
where
1 +
1
2
m > c.
This tells us that the harmonic series diverges.
207
Example 3.3.3
The Harmonic Series
Consider a partial sum of the harmonic series
∞
X
k=1
1
k
.
s
8
=
1
1
+
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
1
7
+
1
8
>
1
1
+
1
2
+
1
4
+
1
4
| {z }
1
2
+
1
8
+
1
8
+
1
8
+
1
8
| {z }
1
2
=1 +
1
2
+
1
2
+
1
2
In general we can make s
n
bigger than any integer c by setting n = 2
m
where
1 +
1
2
m > c.
This tells us that the harmonic series diverges.
207
Example 3.3.3
The Harmonic Series
Consider a partial sum of the harmonic series
∞
X
k=1
1
k
.
s
8
=
1
1
+
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
1
7
+
1
8
>
1
1
+
1
2
+
1
4
+
1
4
| {z }
1
2
+
1
8
+
1
8
+
1
8
+
1
8
| {z }
1
2
=1 +
1
2
+
1
2
+
1
2
In general we can make s
n
bigger than any integer c by setting n = 2
m
where
1 +
1
2
m > c.
This tells us that the harmonic series diverges.
207
Example 3.3.3
The Harmonic Series
Consider a partial sum of the harmonic series
∞
X
k=1
1
k
.
s
8
=
1
1
+
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
1
7
+
1
8
>
1
1
+
1
2
+
1
4
+
1
4
| {z }
1
2
+
1
8
+
1
8
+
1
8
+
1
8
| {z }
1
2
=1 +
1
2
+
1
2
+
1
2
In general we can make s
n
bigger than any integer c by setting n = 2
m
where
1 +
1
2
m > c.
This tells us that the harmonic series diverges.
207
Question 3.3.4
What Is a Geometric Series?
Definition
A geometric series is a series of the form
∞
X
k=1
ar
k−1
.
a is the initial term. r is the common ratio between terms.
Example
∞
X
k=1
1
2
k−1
= 1 +
1
2
+
1
4
+
1
8
+ ···
∞
X
k=1
3
10
1
10
k−1
=
3
10
+
3
100
+
3
1000
+ ··· =
1
3
208
Question 3.3.4
What Is a Geometric Series?
Evaluate
∞
X
k=1
ar
k−1
.
209
Question 3.3.4
What Is a Geometric Series?
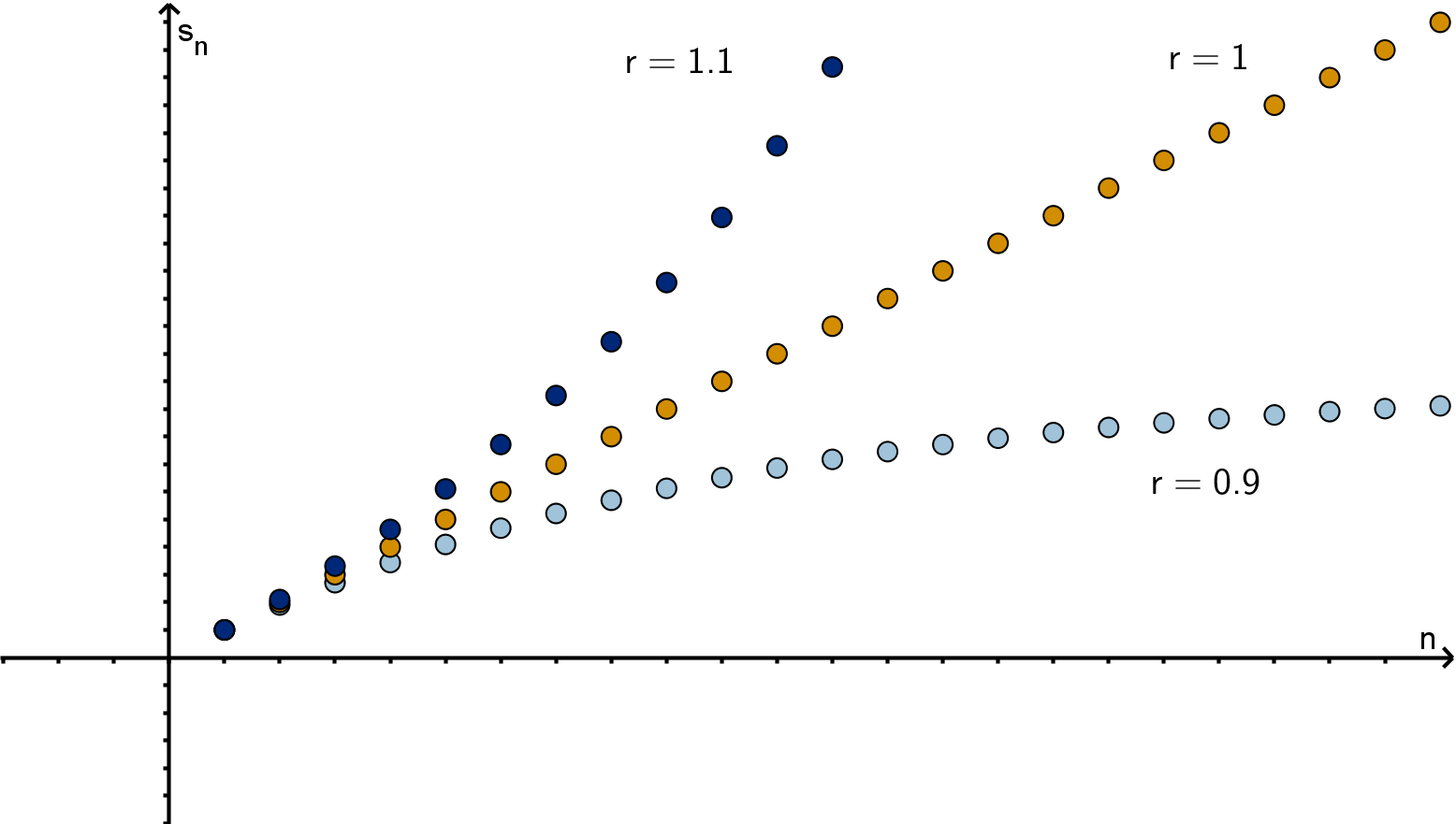
Figure: The partial sums of
P
ar
k−1
for various r
210
Question 3.3.4
What Is a Geometric Series?
Theorem
Geometric series have the following partial sums
s
n
=
n
X
k=1
ar
k−1
=
a(1 − r
n
)
1 −r
if r = 1
an if r = 1
These converge to
a
1 −r
when |r | < 1 and diverge when |r| ≥ 1.
211
Example 3.3.5
Evaluating Geometric Series
Identify a and r in the following geometric series. Then evaluate the
series.
a
2
3
+
4
15
+
8
75
+ ···
b
∞
X
n=2
3
n
c 0.999999 . . .
212
Question 3.3.6
What Does the Size of a
k
Tell Us About
P
a
k
?
Theorem (The Divergence Test)
Let a
k
be a sequence. If lim
k→∞
a
k
= 0, then the series
∞
X
k=1
a
k
diverges.
Remark
The divergence test does not tell us anything, if lim
k→∞
a
k
= 0. The series
might converge, and it might not. In this case we say the test is
inconclusive.
213
Example 3.3.7
Applying the Divergence Test
What does the divergence test tell us about each of the following series?
a
∞
X
k=2
3
k
b
∞
X
k=2
1
k
c
∞
X
k=2
k
2
− 1
3k
2
+ 7
d
∞
X
k=2
k
2
e
k
214
Question 3.3.8
What Is the Ratio Test?
The convergence of a geometric series depends on the ratio r. Even
when a series is not geometric, we can attempt to apply similar reasoning
to determine whether it converges.
Theorem (The Ratio Test)
If lim
k→∞
a
k+1
a
k
= L < 1, then
X
a
k
converges absolutely.
If lim
k→∞
a
k+1
a
k
= L > 1 or is infinite, then
X
a
k
is divergent.
If lim
k→∞
a
k+1
a
k
= 1, then the ratio test is inconclusive.
215
Question 3.3.8
What Is the Ratio Test?
Remark
Converges absolutely is a term for series with both positive and
negative terms. It means the series would converge, even if the signs of
all the terms were all positive. The alternative is conditional
convergence, meaning the series’s convergence may require the positive
and negative terms partially canceling each other out.
Example
The series
1 −
1
2
+
1
3
−
1
4
+
1
5
− ···
converges (we won’t prove this). If we made all the terms positive, it
would be the harmonic series, which diverges. This series converges
conditionally, not absolutely.
216
Example 3.3.9
Applying the Ratio Test
a Does
∞
X
k=1
(−1)
k−1
k!
converge or diverge?
b Does
∞
X
k=1
2
k
k
2
converge or diverge?
c Does
∞
X
k=1
k converge or diverge?
217
Example 3.3.9
Applying the Ratio Test
Main Ideas
When applying the ratio test, be sure to replace every k with k + 1
for the a
k+1
term.
Familiarize yourself with the algebra rules that allow you to simplify
ratios of exponentials and factorials.
218
Example 3.3.10
A Strategy for Series Tests
Strategy
Given the three ways we have to test for divergence and convergence and
the relative ease of applying each, here is a reasonable approach to
testing a series.
Check lim
n→∞
a
n
by dominance
Compute
a
n+1
a
n
Compute lim
n→∞
a
n+1
a
n
P
a
n
converges
P
a
n
diverges
Inconclusive, look up another test
not zero
zero
hard to tell
constant |r | ≥ 1 constant |r | < 1
not constant
< 1> 1
= 1
hard to tell
219
Example 3.3.10
A Strategy for Series Tests
Let’s apply our strategy to see what we can tell about
∞
X
n=1
1
n
2
.
220
Section 3.3
Summary Questions
Q1 What is the difference between a sequence and a series?
Q2 How do we evaluate a series?
Q3 What is a geometric series. How do we evaluate one?
Q4 What does it mean to say that a series test is inconclusive?
Q5 How do each of the following factors behave in the ratio
a
k+1
a
k
?
a k
p
(p a constant)
b c
k
(c a constant)
c k!
Q6 How would the ratio test apply to a geometric series
X
ar
k−1
?
221
Section 3.3
Q52
Suppose that a discrete random variable X has distribution function
f
X
(x) =
(
1
x
−
1
x+1
if x is a positive integer
0 otherwise
a Verify that f
X
(x) is a valid probability distribution function.
b Compute P(3 ≤ X ≤ 5).
c Explain why you can’t compute E[X ].
222
Section 3.4
Power Series
Goals:
1 Use series tests to determine for what values of x a power series
converges.
2 Identify the radius of convergence of a power series.
3 Recognize functions that can be rewritten as a power series.
Question 3.4.1
What Is a Power Series?
So far we have studied infinite series of numbers. If instead of just
numbers, our terms include variables, then we’ve created a function.
Plugging in different values for the variable gives us a different series of
numbers.
Example
The expression
1 + x + x
2
+ x
3
+ ···
becomes
1 + 2 + 4 + 8 + ···
when we evaluate it at x = 2. It becomes
1 −
1
3
+
1
9
−
1
27
+ ···
when we evaluate it at x = −
1
3
.
224
Question 3.4.1
What Is a Power Series?
Definition
An infinite series of the form
∞
X
k=0
c
k
(x − a)
k
is called a power series centered at a.
It is a function of x whose domain is all values of x that make the series
converge.
For the purposes of this definition, we define x
0
= 1 even when x = 0.
225
Example 3.4.2
A Geometric Series as a Power Series
Use the geometric series formula to write f (x) =
1
1 −x
as a power series
and find its domain.
226
Example 3.4.3
The Domain of a Power Series
What is the domain of
∞
X
k=1
k
2
4
k
(x − 5)
k
?
227
Example 3.4.3
The Domain of a Power Series
Main Idea
The ratio test is usually successful in finding where a power series
converges. Generally it is inconclusive at only two points. We will not
always have a test that can tell us whether the series converges at these
points.
228
Example 3.4.3
The Domain of a Power Series
Theorem
Given a power series
∞
X
k=0
c
k
(x − a)
k
centered at a, one of the following is
true.
1 The series converges only when x = a.
2 The series converges when x is any real number.
3 There is a radius of convergence R such that
a The series converges when |x − a| < R, and
b The series diverges when |x − a| > R.

Figure: The domain |x − a| < R of a power series.
229
Question 3.4.4
Can We Integrate or Differentiate a Power Series?
When f (x) is a polynomial, we can find the derivative and anti-derivative
of f (x) by computing the (anti-)derivative of each term. The following
theorem says that we can do this for a power series too.
Theorem
If f (x) is the power series
∞
X
k=0
c
k
(x − a)
k
and f (x) has radius of
convergence R > 0 then f (x) is differentiable and continuous on the
interval (a − R, a + R), and
1 f
′
(x) =
∞
X
k=1
kc
k
(x − a)
k−1
2
Z
f (x) dx = C +
∞
X
k=0
c
k
(x − a)
k+1
k + 1
Both of these functions also have radius of convergence R.
230
Question 3.4.4
Can We Integrate or Differentiate a Power Series?
Example
We have seen that
1
1 −x
=
∞
X
k=0
x
k
on the interval (−1, 1). From that we
can compute:
d
dx
∞
X
k=0
x
k
=
∞
X
k=1
kx
k−1
Z
∞
X
k=0
x
k
dx =
∞
X
k=0
x
k+1
k + 1
+ c
Both have domain (−1, 1).
231
Section 3.4
Summary Questions
Q1 What is the difference between a polynomial and a power series?
Q2 What test is useful for establishing the domain of a power series?
What form can this domain have?
Q3 How can we integrate or differentiate a power series?
Q4 How does differentiation affect the radius of convergence of a power
series?
232
Section 3.4
Q18
Suppose you are told that a given power series p(x) centered at x = a
converges at x = −4 and diverges at x = −7.
a If a = 1, what can you say about the domain of p(x)?
b What are all of the the possible values of a? Explain your reasoning
(briefly).
233
Section 3.5
Taylor Series
Goals:
1 Use a combination of power series and algebra to work with
functions.
2 Integrate and differentiate power series.
Question 3.5.1
What Is a Taylor Series?
Definition
The Taylor series of f (x) at x = a is
T (x) =
∞
X
k=0
f
(k)
(a)
k!
(x − a)
k
.
The Taylor series’s partial sums s
n
are the Taylor polynomials T
n
(x) of f
at x = a.
Remark
Several mathematicians contributed to the discovery of Taylor series.
Taylor series centered at x = 0 were popularized by Colin Maclaurin, and
so are often called Maclaurin series.
235
Question 3.5.1
What Is a Taylor Series?
Limitations of Taylor Series
Taylor polynomials were designed to approximate f (x). We might hope
that T (x) would be the perfect approximation, that T (x) and f (x) are
equal. Unfortunately, there are obstacles to this.
The Taylor series might not converge for all x.
The Taylor polynomials might not approximate f (x) very well at all.
Recall our example
f (x) =
(
0 if x ≤ 0
e
−
1
x
if x > 0
For this function T (x) = 0.
236
Example 3.5.2
Writing a Taylor series
Let f (x) = e
x
a Find the Taylor series for f (x) centered at x = 0.
b On what interval does it converge?
237
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
Let f (x) = ln x
a Find a pattern in the derivatives and write a general expression for
the kth derivative: f
(k)
(x).
b Use your answer to a to write expressions for the Taylor
polynomials T
n
(x) and the Taylor series T (x) of ln x centered at 1.
Simplify the coefficients if possible.
c What does the ratio test tell you about where T (x) converges?
d If we wanted to apply Taylor’s inequality to T
n
(x), we would need to
know where the derivative is largest (in absolute value). Where is the
(n + 1)th derivative largest on the interval [x, 1]? (Here 0 < x < 1).
e Where is the (n + 1)th derivative largest on the interval [1, x]?
(Here x > 1).
f What does Taylor’s inequality say about where R
n
(x) → 0 as
n → ∞?
g What does our answer to the previous question tell us about T (x)?
238
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
a Find a pattern in the derivatives and write a general expression for
the kth derivative: f
(k)
(x).
238
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
b Use your answer to a to write expressions for the Taylor
polynomials T
n
(x) and the Taylor series T (x) of ln x centered at 1.
Simplify the coefficients if possible.
238
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
c What does the ratio test tell you about where T (x) converges?
238
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
d If we wanted to apply Taylor’s inequality to T
n
(x), we would need to
know where the derivative is largest (in absolute value). Where is the
(n + 1)th derivative largest on the interval [x, 1]? (Here 0 < x < 1).
238
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
e Where is the (n + 1)th derivative largest on the interval [1, x]?
(Here x > 1).
238
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
f What does Taylor’s inequality say about where R
n
(x) → 0 as
n → ∞?
238
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
g What does our answer to the previous question tell us about T (x)?
238
Synthesis 3.5.3
Is a Taylor Series Equal to the Function it Approximates?
Figure: The Taylor polynomials approach ln x only on (0, 2].
239
Example 3.5.4
Mixing Taylor Series and Algebra
Let f (x) = x
2
sin x. Compute a Taylor series for f (x) centered at x = 0.
240
Example 3.5.4
Mixing Taylor Series and Algebra
Main Idea
When constructing a Taylor series for f (x) = x
k
g(x) centered at 0,
construct the Taylor series of g(x), and then distribute the x
k
.
241
Example 3.5.5
Integrating a Taylor Series
Let f (x) = e
x
2
.
a Write a Taylor polynomial T
4
(x) for f (x) at x = 0.
b Find a better way to produce the Taylor series for f (x).
c Compute a Taylor series for
Z
e
x
2
dx.
242
Example 3.5.5
Integrating a Taylor Series
a Write a Taylor polynomial T
4
(x) for f (x) at x = 0.
242
Example 3.5.5
Integrating a Taylor Series
b Find a better way to produce the Taylor series for f (x).
242
Example 3.5.5
Integrating a Taylor Series
b Compute a Taylor series for
Z
e
x
2
dx.
242
Example 3.5.5
Integrating a Taylor Series
Figure: The graph of e
x
2
,
R
e
x
2
dx, and the partial sums of its Taylor series.
Main Ideas
Compositions of functions can be composed through Taylor series.
Taylor series allow us to integrate functions that are otherwise
impossible to integrate.
243
Application 3.5.6
Euler’s Formula
Recall i is an imaginary number that satisfies i
2
= −1.
a Find an expression for f (x) = e
ix
.
b Write your answer in terms of the Taylor series for sin x and cos x.
c Write two different expressions for e
i2x
. How is this equation useful?
244
Section 3.5
Summary Questions
Q1 How can we be sure that a Taylor series converges to the function it
is approximating?
Q2 What is the domain of a Taylor series?
Q3 How can we produce the Taylor series for x
n
f (x) or f (x
n
)? Where
does the center need to be for the result to be a Taylor series?
Q4 What is a Maclaurin series?
245
Section 3.5
Q16
Suppose for a function f we are able to place a bound of
k!
3
k
on the kth
derivative of f over any interval. For what values of x can we conclude
that T (x), the Taylor series centered at 2, is equal to f (x)?
246
Section 3.5
Q18
For a general function f and its Taylor polynomials and series, how are
the following sets of points related? Does every number belonging to one
of these sets belong to one of the others?
The set of numbers x where T (x) converges.
The set of numbers x where |R
n
(x)| → 0 as n → ∞.
The set of numbers where f (x) = T (x).
247
Section 3.5
Q26
Write the Taylor series for f (x) =
1
x
centered at 1. Verify that one of its
antiderivatives is a Taylor series for ln x.
248
Section 3.5
Q34
Suppose we have a function f (x) and two different numbers a and b.
Suppose further that the Taylor series for f (x) centered at a is equal to
the Taylor series for f (x) centered at b. What can you say about the
domain of this Taylor series?
249