Chapter 4
Multivariable Functions
This chapter introduces functions of more than one variable. We construct the higher dimensional spaces
needed for their domains, we produce tools to visualize them, and we compute their rates of change.
Contents
4.1 Three-Dimensional Coordinate Systems . . . . . . . . . . . . . . . . . . . . 242
4.2 Functions of Several Variables . . . . . . . . . . . . . . . . . . . . . . . . . . 259
4.3 Limits and Continuity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 275
4.4 Partial Derivatives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 281
4.5 Linear Approximations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 295
Section 4.1
Three-Dimensional Coordinate Systems
Goals:
1 Plot points in a three-dimensional coordinate system.
2 Use the distance formula.
3 Recognize the equation of a sphere and find its radius and center.
4 Graph an implicit function with a free variable.
Suppose we wanted to understand the growth rate of a species of bacteria. We could grow several
dozen cultures and take a series of measurements of size s at times t of each. Each measurement is an
ordered pair (t, s). We can plot these pairs in a coordinate plane to get a visual sense of how growth
occurs over time. We might even fit a function that approximates s as a function of t. What if we wanted
to understand the role of some other measurement, like temperature, light, or the availability of various
food sources? We could grow many cultures in different conditions. Now a single measurement has three
or more pieces of information. While we could strip these out and plot our data on a temperature/size
coordinate plane, we risk missing important relationships with the other variables. In order to take
advantage of the visual and computational benefits of a coordinate system, we must be prepared to
work with a coordinate system of more than two variables.
Question 4.1.1
How Do Cartesian Coordinates Extend to Higher Dimensions?
The best way to define a higher-dimensional coordinate system is to extrapolate from the coordinate
plane. This way we don’t need to remember a set of novel and arbitrary rules, and our two-dimensional
experience will be a guide to us in dimensions where we have no visual intuition.
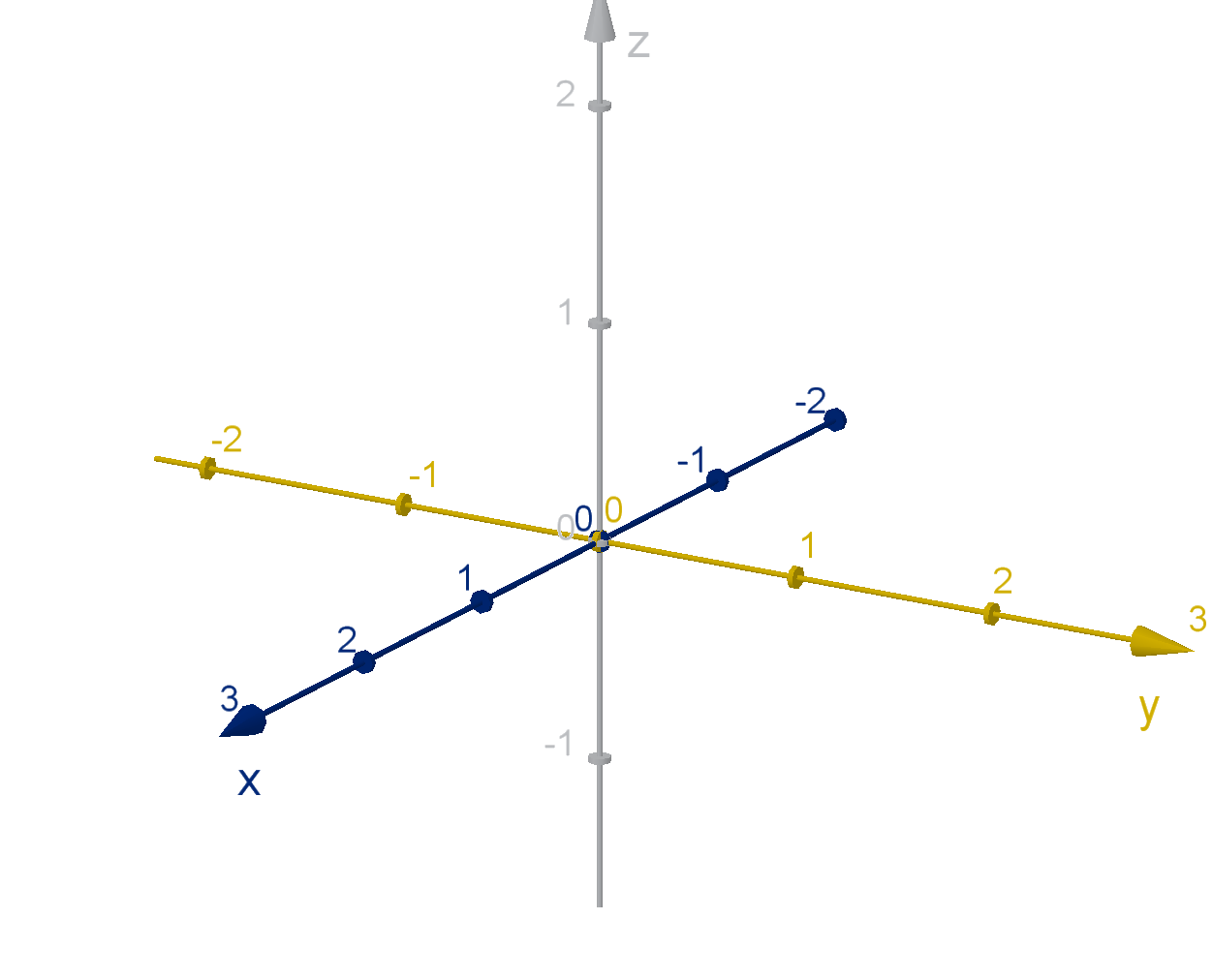
Recall how we constructed the Cartesian plane.
x
y
−4
−4
−3
−3
−2
−2
−1
−1
1
1
2
2
3
3
4
4
(2, 3)
1 Assign origin and two directions (x, y).
2 y is 90 degrees anticlockwise from x.
3 Axes consist of the points displaced in only one direction.
4 Coordinates refer to displacement from the origin in each
direction.
5 Either displacement can happen first.
6 Each point has exactly one ordered pair that refers to it.
In a three-dimensional Cartesian coordinate system. We can extrapolate from two dimensions.
242
1 Assign origin and three directions (x, y, z).
2 Each axis makes a 90 degree angle with the
other two.
3 The z direction is determined by the right-
hand rule.
Question 4.1.2
How Do We Establish Which Direction Is Positive in Each Axis?
The choice of which direction is positive is arbitrary. However, it is important that we all make the
same choice, or our visualizations will be incompatible. In two dimensions, we agree that the positive
y-axis is counterclockwise from the positive x-axis. This will not work in three dimensions. Suppose the
positive y-axis is counterclockwise from the positive x-axis in three-space. If you rotate your point of
view to see the axes from the other side, the positive y-axis is now clockwise from the positive x-axis.
Thus the relative orientation of the positive x and y directions does not matter. You could pick a
different orientation, and just be looking at three-space from a different viewpoint.
The z direction is different. Once we’ve chosen a positive x and y direction, there are two equally
valid possible directions for positive z, pointing in opposite directions from each other. The choice here
matters, but it will be arbitrary. We agree to define the positive z direction by the right hand rule.
The right hand rule says that if you make the fingers of your right hand follow the (counterclockwise)
unit circle in the xy-plane, then your thumb indicates the direction of the positive z-axis.
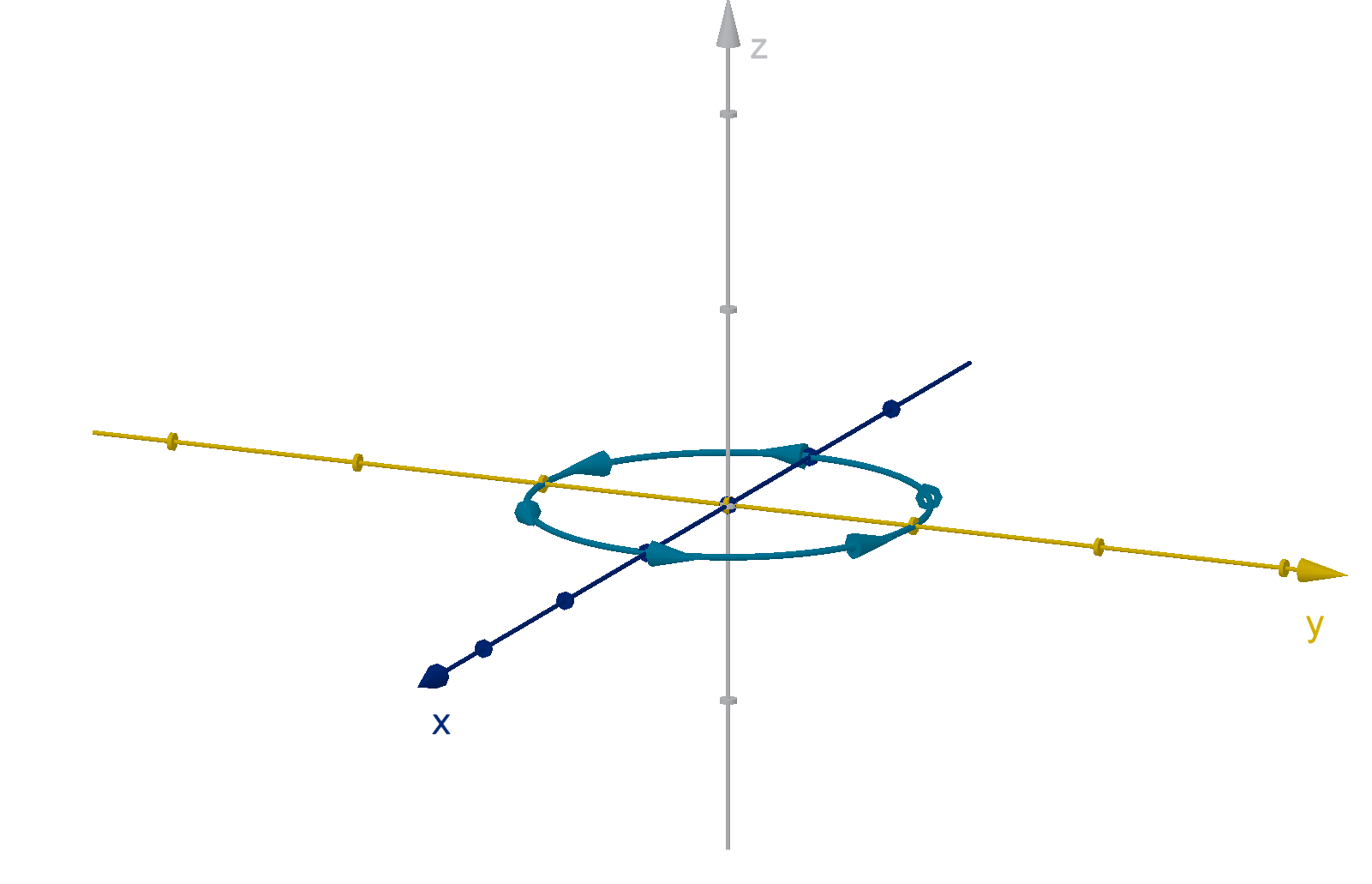
Figure: The counterclockwise unit circle in the xy-plane
243
Example 4.1.3
Drawing a Location in Three-Dimensional Coordinates
The point (2, 3, 5) is the point displaced from the origin by
2 in the x direction
3 in the y direction
5 in the z direction.
How do we draw a reasonable diagram of where this point lies?
Solution
We can begin by finding the points (2, 0, 0) which lies on the x-axis two units from the origin and
(0, 3, 0) which lies on the y-axis three units from the origin. Along with the origin itself, these points
and (2, 3, 0) form a parallelogram. Now we need a displacement of 5 in the z direction. We can copy
the length and direction of this displacementof the segment from (0, 0, 0) to (0, 0, 5) on the z-axis. We
draw a segment of that length and direction from (2, 3, 0). The top of this segment is (2, 3, 5).
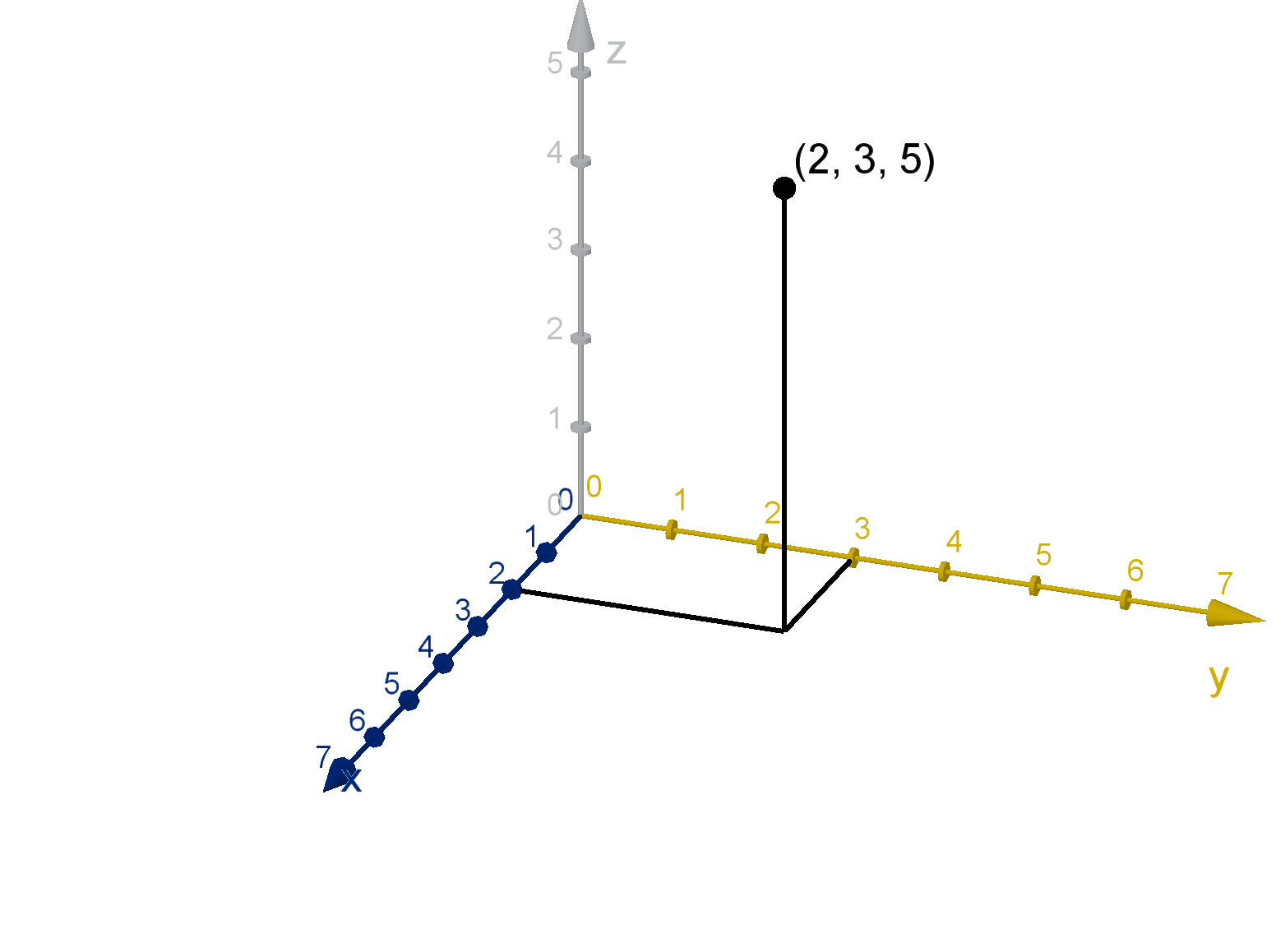
Remark
The extra lines we used to construct (2, 3, 5) are not just useful for guaranteeing accuracy, they also help
our audience to correctly visualize the location we mean to plot. When we project three-space onto a
flat page, each point on the page represents infinitely many points stretching into the background. If we
only draw a isolated point, which of these are we representing? Lines like the ones we produced in this
example trick a viewers brain into visualizing correct three-dimensional location in our flat diagram.
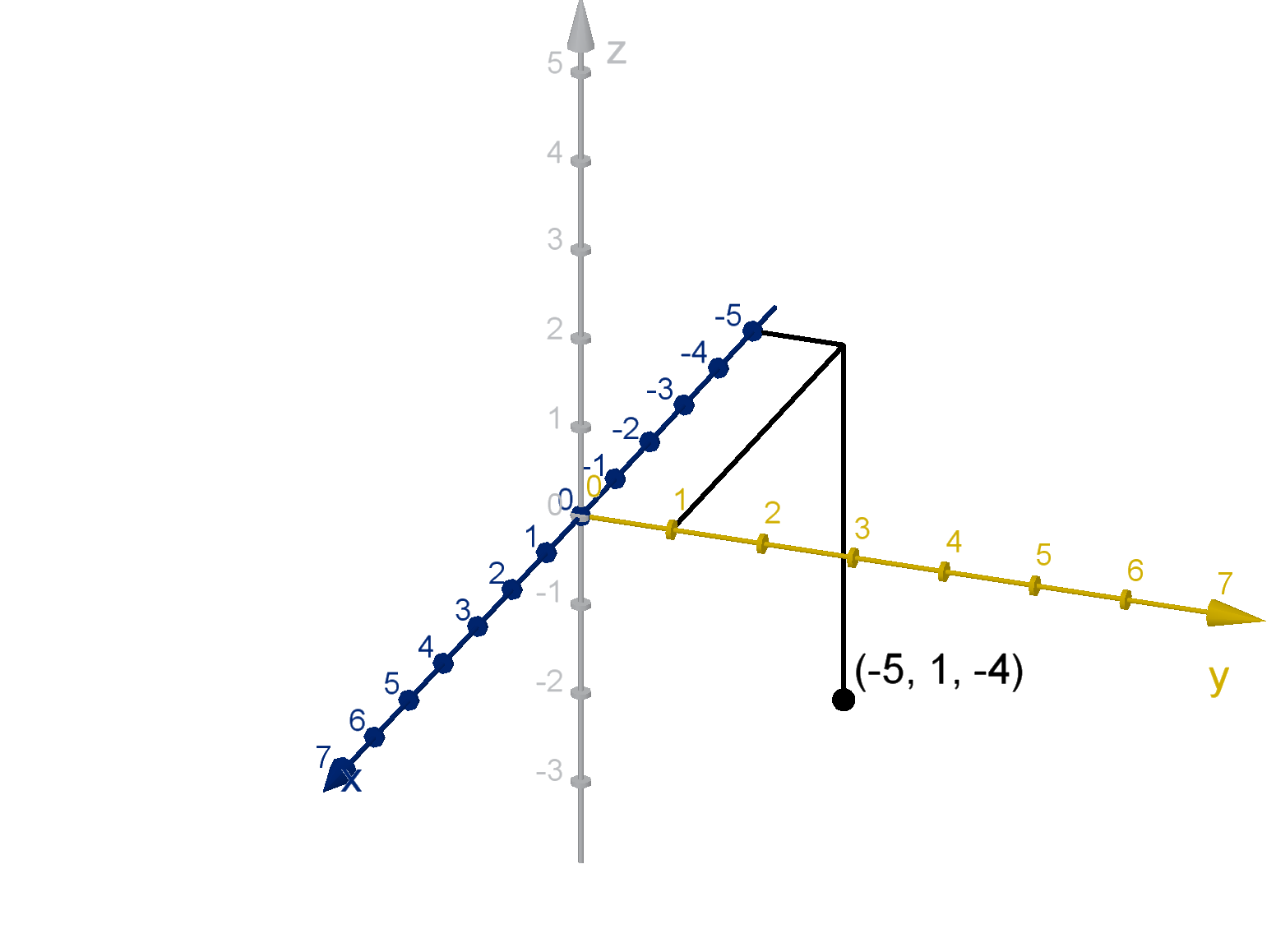
How can we draw a reasonable diagram of (−5, 1, −4)?
244
Solution
The procedure here is the same, except that the displacements in the x and z directions are negative.
Thus when producing these displacements, we travel backward along their axes.
Question 4.1.4
How Do We Measure Distance in Three-Space?
Since coordinate displacements in two-space are perpendicular, we compute the distance to a point
using the Pythagorean theorem. This reasoning extends to higher dimensions, but we need to build the
correct length using two or more right triangles.
Theorem
The distance from the origin to the point (x, y, z) is given by the Pythagorean Theorem
D =
p
x
2
+ y
2
+ z
2
245
Question 4.1.4
How Do We Measure Distance in Three-Space?
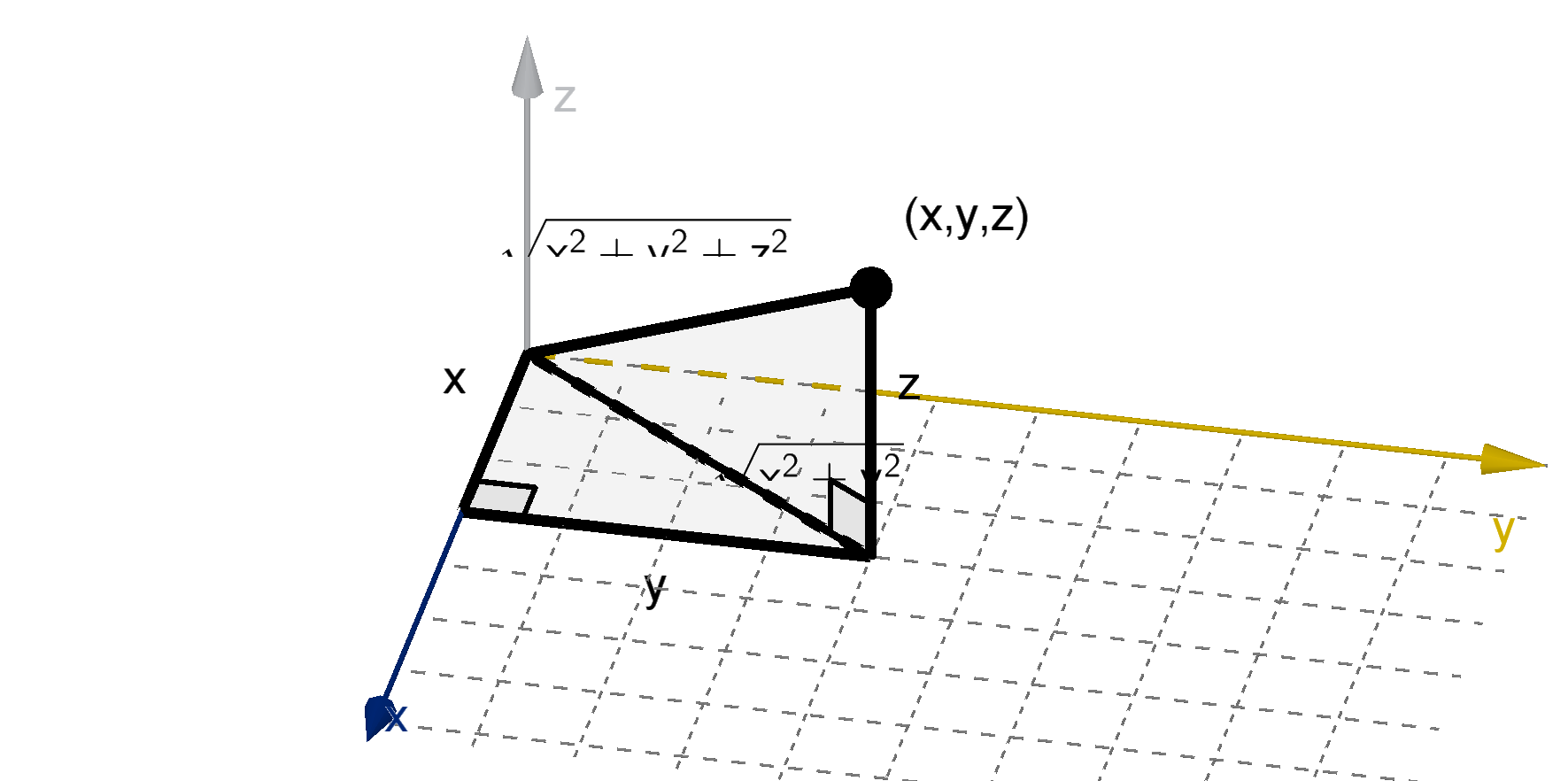
We first compute the distance from the origin to (x, y, 0) using a right triangle in the xy-plane.
The right triangle with the vertices (0, 0, 0), (x, y, 0) and (x, y, z) allows us to apply the Pythagorean
theorem again.
D
2
=
p
x
2
+ y
2
2
+ z
2
If neither of the points is the origin, we can compute the displacements by subtraction. This is a
natural extension of the two-space distance formula.
Theorem
The distance from the point (x
1
, y
1
, z
1
) to the point (x
2
, y
2
, z
2
) is given by
D =
p
(x
1
− x
2
)
2
+ (y
1
− y
2
)
2
+ (z
1
− z
2
)
2
Question 4.1.5
What Is a Graph?
A well-prepared calculus student has learned to understand the graphs of many equations: lines,
circles, parabolas. The definition of a graph, on the other hand, is often discarded after a few exercises
of plotting points by hand. The definition is worth recalling. It applies to a space of any dimension.
Definition
The graph of an implicit equation is the set of points whose coordinates satisfy that equation. In other
words, the two sides are equal when we plug the coordinates in for x, y and z.
This definition allows us to immediately understand the graphs of some equations. The graph of
the following equation consists of the points that, when plugged into a specific distance formula and
squared, give a result of 9. This is a sphere.
246
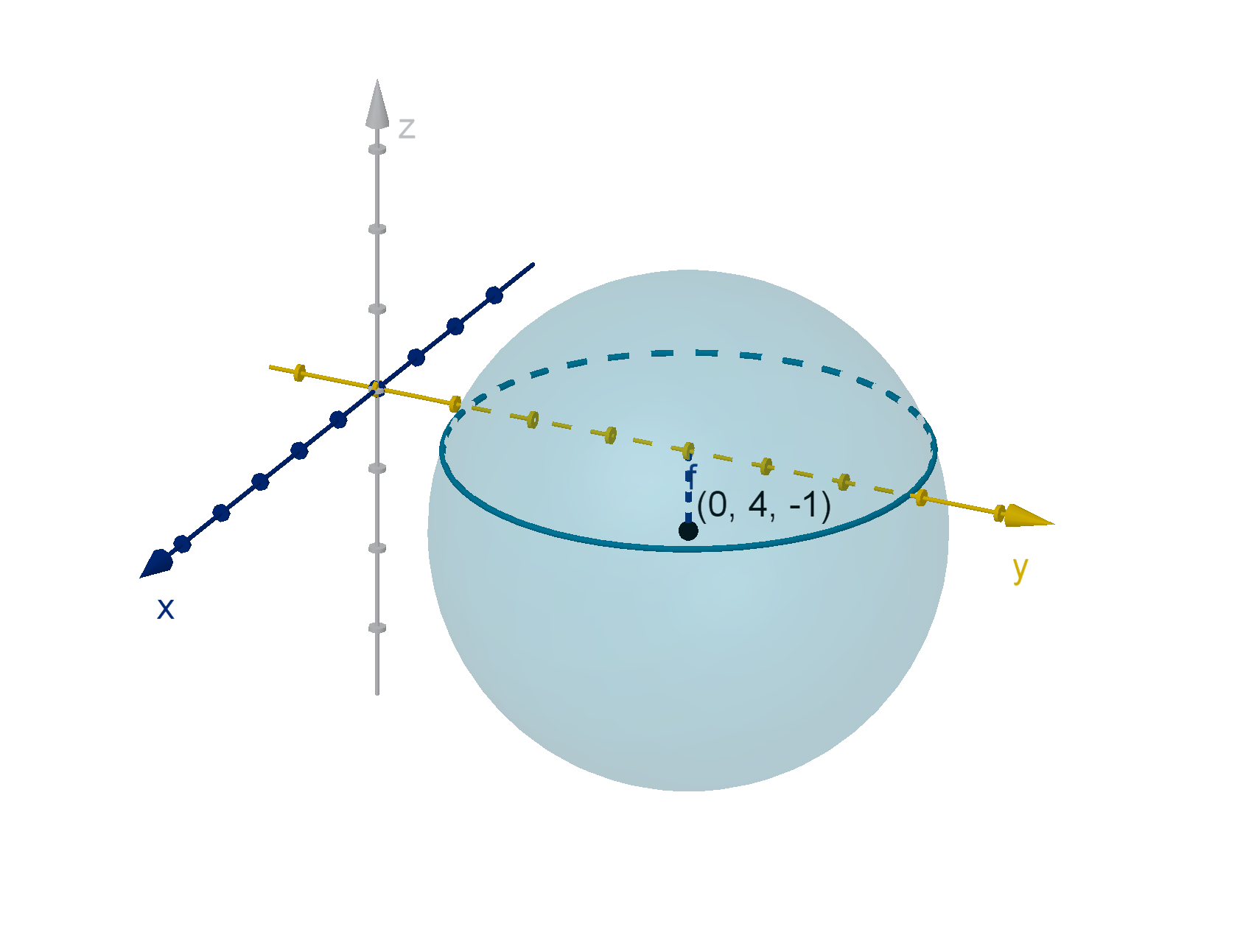
Example
The graph of
x
2
+ (y −4)
2
+ (z + 1)
2
= 9
is the set of points that are distance 3 from the point
(0, 4, −1)
Example 4.1.6
Graphing an Equation with Two Free Variables
Sketch the graph of the equation y = 3.
Solution
The naive approach would have us seek out the point marked with 3 on the y-axis. However, in two-
space, we know that the graph would be a horizontal line, not just the point (0, 3). Why is this? Any
point of the form (x, 3) satisfies the equation y = 3. Similarly, any point of the form (x, 3, z) in three-
space satisfies y = 3. These are all the points that can be reached from (0, 3, 0) by displacements in
the x and z directions. They create a plane through (0, 3, 0) parallel to the x and z axes.
Much as lines are the simplest and most fundamental one-dimensional objects, planes are the simplest
and most fundamental two-dimensional objects. In addition to coordinate axes, 3-dimensional space has
3 coordinate planes.
1 The graph of z = 0 is the xy-plane.
2 The graph of x = 0 is the yz-plane.
3 The graph of y = 0 is the xz-plane.
247
Example 4.1.6
Graphing an Equation with Two Free Variables
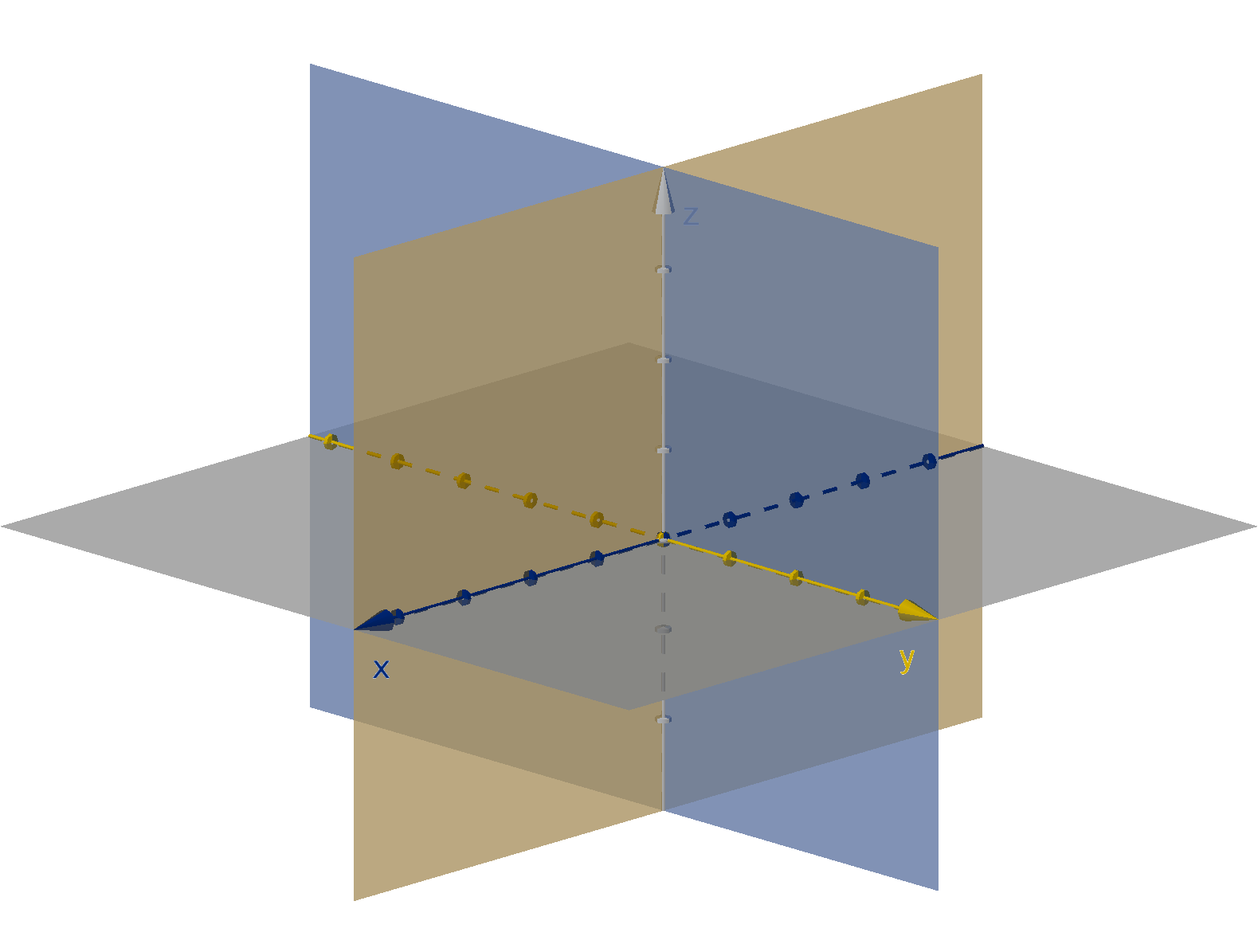
Figure: The coordinate planes in 3-dimensional space.
Remark
Planes extend forever but our pictures of them cannot. Notice that graphing software cuts them off
parallel to the axes they contain. The resulting images are parallelograms. This is a good practice when
drawing planes by hand too. It suggests the proper orientation to the viewer, despite the limitations of
a flat visualization.
Example 4.1.7
Graphing an Equation with One Free Variable
Sketch the graph of the equation z = x
2
− 3.
Solution
We should recognize this as the equation of a parabola. If we ignore the variable y, we can graph this
equation in the xz plane. What does the absence of absence of y in the equation mean? If we follow
the definition of a graph, the value of y has no effect on whether a point lies on the graph or not. We
can take the parabola in the xz plane, and project it in the y direction to obtain a surface called a
parabolic cylinder.
248
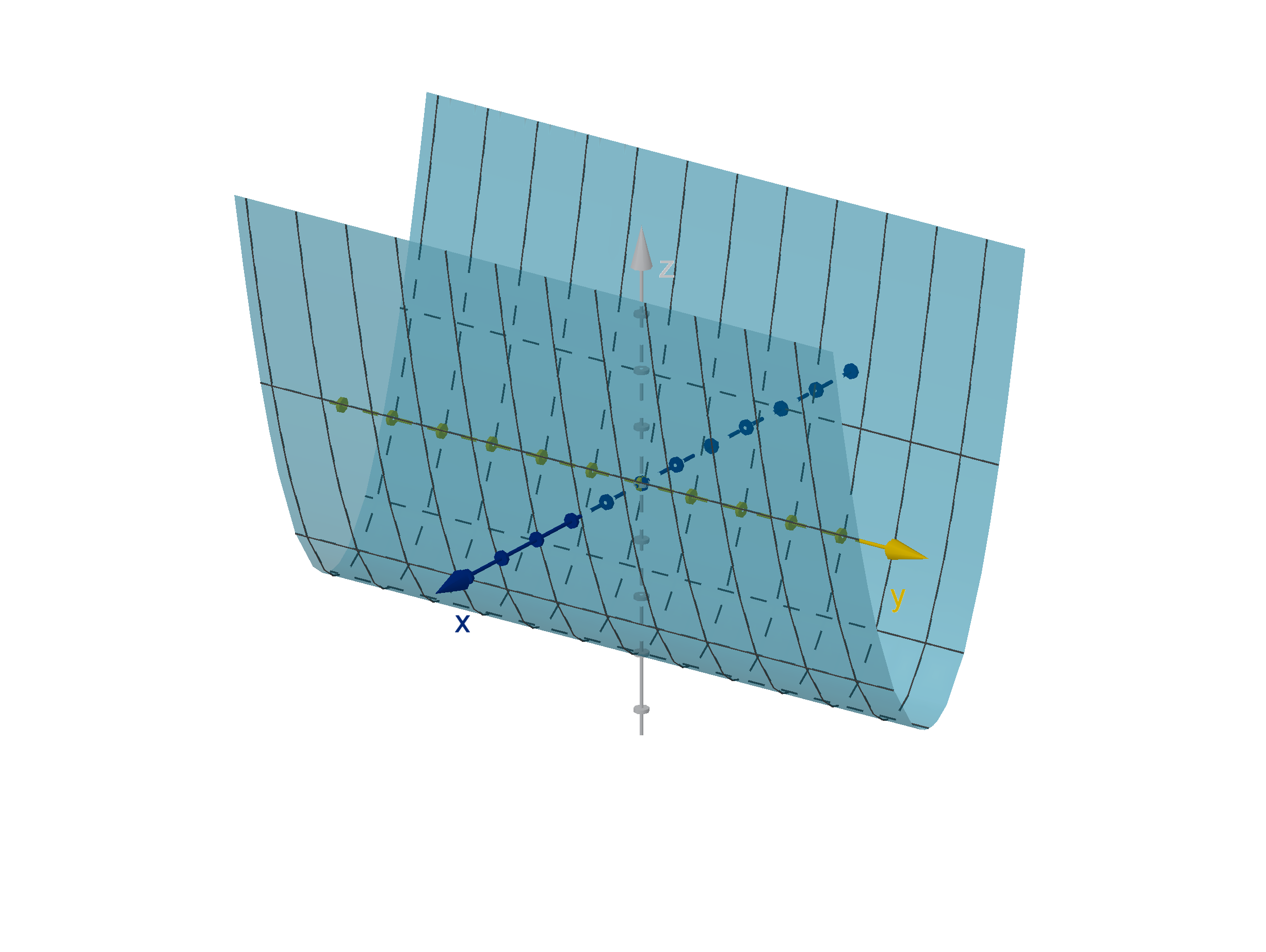
z = x
2
− 3
Question 4.1.8
What Do the Graphs of Implicit Equations Look Like Generally?
Notice that the graph of an implicit equation in the plane is generally one-dimensional (a curve),
whereas the graph of an implicit equation in three-space is generally two-dimensional (a surface).
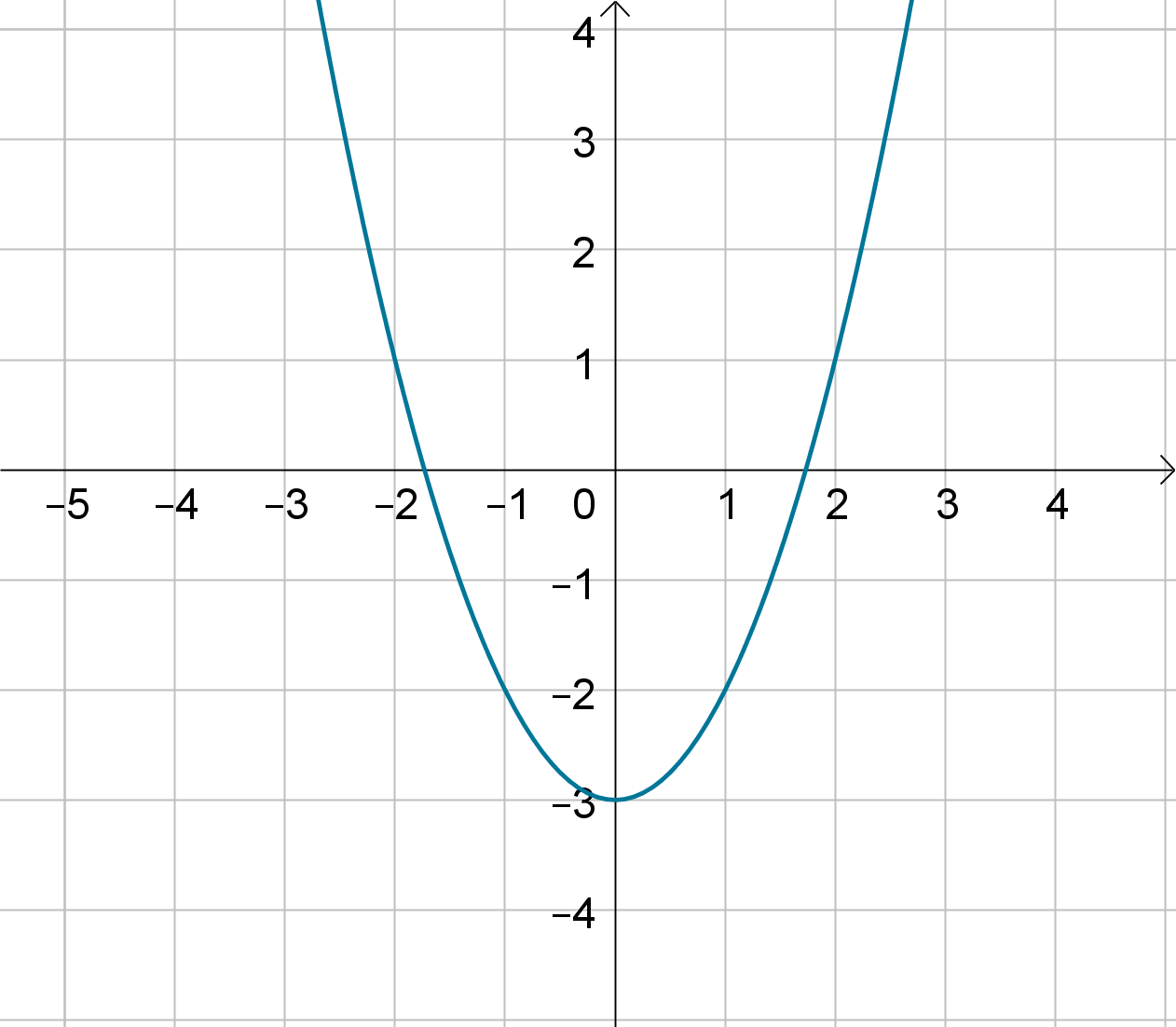
Figure: The curve y = x
2
− 3

Figure: The surface z = x
2
− 3
Question 4.1.9
What Is the Slope-Intercept Equation of a Plane?
Unlike a line, a non-vertical plane has two slopes. One measures rise over run in the x-direction, the
other in the y-direction.
249
Question 4.1.9
What Is the Slope-Intercept Equation of a Plane?
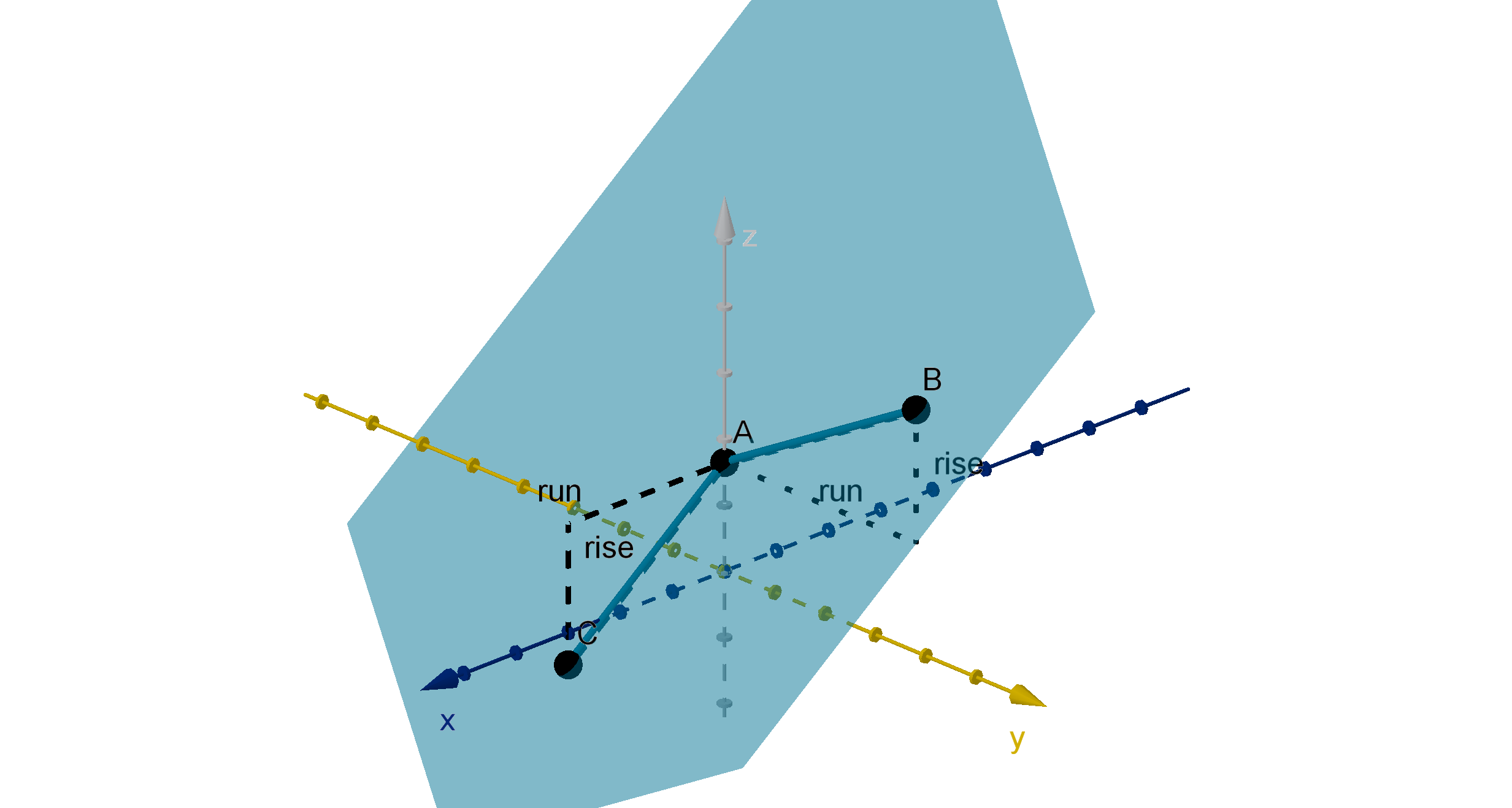
Figure: A plane with slopes in the x and y directions.
Equation
A plane with z intercept (0, 0, b) and slopes m
x
and m
y
in the x and y directions has equation
z = m
x
x + m
y
y + b.
Example 4.1.10
Writing the Equation of a Plane
Write the equation of a plane with intercepts (4, 0, 0), (0, 6, 0) and (0, 0, 8).
Solution
From the point (4, 0, 0) to the point (0, 0, 8), the plane rises by 8 while x is reduced by 4. This gives a
slope in the x direction.
m
x
=
8 − 0
0 − 4
= −2.
Similarly,
m
y
=
8 − 0
0 − 6
= −
4
3
.
The point (0, 0, 8) is on the z-axis, and so indicates that the z-intercept is 8. Combining these, we
conclude the plane has equation:
z = −2x −
4
3
y + 8
250
Main Idea
Given three points in a plane A = (x
1
, y
1
, z
1
), B = (x
2
, y
2
, z
2
) and C = (x
3
, y
3
, z
3
)
1 If two points share an x-coordinate, we can directly compute m
y
and vice versa.
2 Failing that, we can set up a system of equations and solve for m
x
, m
y
and b.
Question 4.1.11
How Do We Extrapolate to Even Higher Dimensions?
The measurements we take of each observation, the more dimensions we need to plot the data we
have produced. Extrapolating from three-space to even higher dimensions introduces no new difficulties,
except that we cannot visualize the result. We can use a coordinate system to describe a space with
more than 3 dimensions. k-dimensional space can be defined as the set of points of the form
P = (x
1
, x
2
, . . . , x
k
).
Theorem
The distance from the origin to P = (x
1
, x
2
, . . . , x
k
) in k-space is
q
x
2
1
+ x
2
2
+ ··· + x
2
k
There is no right hand rule for higher dimensions, because we can’t draw these spaces anyway.
251
Section 4.1
Exercises
Summary Questions
Q1
What displacements are represented by the notation (a, b, c)?
Q2
What is the right hand rule and what does it tell you about a three-dimensional coordinate
system?
Q3
In three-space, what is the y-axis? What are the coordinates of a general point on it?
Q4
In three space, what is the xz-plane? What are the coordinates of a general point on it? What
is its equation?
Q5
How do we use a free variable to sketch a graph?
Q6
How do we recognize the equation of a sphere?
4.1.1
Q7
Suppose that instead of denoting each point P = (x, y) in R
2
by its displacements from the
origin in the x- and y-directions, we denote it by P = (d, m) where d is its distance from the
origin, and m is the slope of the line through P and the origin. What problems could arise from
adopting this convention?
Q8
Suppose the x and y axes were not perpendicular. Could we still assign coordinates to each point
by its x and y displacements from the origin? Demonstrate with a diagram.
252
4.1.2
Q9
Which of the following depictions of the xy-plane are consistent with the usual orientation, and
which are backwards?
a
The positive x axis points up, and the positive y-axis points left.
b
The positive x axis points down, and the negative y-axis points right.
c
The positive x axis points left, and the positive y-axis points up.
d
The negative x axis points right, and the positive y-axis points down.
e
The positive x axis points up and to the right, and the positive y-axis points down and to
the right.
Q10
Suppose we draw the xy plane on our paper in the standard way, and our paper is lying on a
table. Does the z-axis point down into the table or up out of the table?
4.1.3
Q11
Draw diagrams of points with the following coordinates.
a
(6, 1, 2)
b
(−3, 0, 0)
c
(2, −1, 4)
d
(0, 3, 5)
Q12
Draw diagrams of points with the following coordinates.
a
(−4, 0, 0)
b
(3, −2, 0)
253
Section 4.1
Exercises
c
(4, 5, −3)
d
(−1, 3, 4)
4.1.4
Q13
Compute the distance between (3, 6, 2) and (7, 3, −10).
Q14
Compute the distance between (0, 3, 2) and (5, 1, 0).
Q15
Compute the distance between (10, 12, 109) and (11, 9, 105).
Q16
Compute the distance between (53, 42, 9) and (43, 78, 2).
4.1.5
Q17
Does the point (4, 3, 8) lie on the graph of z = x
2
− 2? Explain how you know.
Q18
Does (2, 2, 1) lie on the graph of x
2
+ y
2
+ z
2
= 9? Explain how you know.
Q19
What is the graph of y
2
+ z
2
= −1? Explain your reasoning.
Q20
The point (2, 3, 4) lies on the graph ax + ay − z = 26. What is the value of the number a?
Q21
Olivia says that the graph of (x−2)(y −3) = 0 in the xy-plane is the point (2, 3). Do you agree?
How would you explain it?
Q22
How is the graph of f(x, y, z)g(x, y, z) = 0 related to the graphs of f(x, y, z) = 0 and g(x, y, z) =
0?
254
4.1.6
Q23
Does the graph of z = 4 intersect the graph of z = 6? Explain both using geometry and algebra.
Q24
Does the graph of x = 2 intersect the graph of z = 1? Explain.
4.1.7
Q25
Sketch the graph of each equation.
a
x = −4
b
x
2
+ y
2
= 9
c
x
2
+ 4x + y
2
+ z
2
− 2z = 4
Q26
Sketch a graph of z = −2.
Q27
Sketch a graph of y = −z
2
.
Q28
Sketch a graph of x
2
+ z
2
= 25.
4.1.8
Q29
What dimension you we expect the graph of an equation to be in 6-dimensional space?
Q30
What is the graph of x
2
+ y
2
= 0 in the xy-plane? Is this an exception to our intuition about
the dimension of a graph?
Q31
Zoe and Muhammad both sketch the graph of y = x
2
. Zoe’s graph is a curve. Muhammad’s is
a surface. Has one of them drawn the wrong graph? Explain.
Q32
In R
3
, what is the dimension of the intersection of the graphs x
2
+ y
2
= 25 and z = 1? Can you
explain this in terms of our intuition about the dimension of a graph.
255
Section 4.1
Exercises
4.1.9
Q33
Suppose that y is a free variable in the equation of a plane. What does that tell us about m
x
and m
y
?
Q34
Gabby is trying to find the equation of a plane P , but she doesn’t know any points on the xz-plane
or yz-plane. Instead she knows that P contains the points:
A = (1, 3, 6) B = (5, 3, 4) C = (7, 5, 10)
Using points A and B, she decides that m
x
=
4−6
5−1
= −
1
2
. Using points A and C, she decides
that m
y
=
10−6
5−3
= 2.
a
Which of Gabby’s conclusions do you agree with and which do you disagree with? Why?
b
How could you fix the one that is wrong?
Q35
Supoose you intend to write the equation of the plane through A, B and C in slope-intercept
form. If A = (3, 5, 7) and B = (3, 2, 4), what value(s) of the y coordinate of C would make it
easiest to compute m
x
?
Q36
Recall that we can write the equation of a line in R
2
in point-slope form:
y −y
0
= m(x − x
0
)
where m is the slope and (x
0
, y
0
) is a known point. This was especially useful in single-variable
calculus for writing equations of tangent lines.
a
How would you expect to write the equation of the plane P through (2, 4, −6) with slopes
m
x
=
1
2
and m
y
= −3?
b
Does your answer to
a
actually pass through (2, 4, −6)? How do you know?
c
Is your answer to
a
actually the equation of a plane? How do you know? Does it have the
correct slopes?
d
Write a general expression for point-slope form for a plane.
Q37
The plane P has slopes m
x
= 3 and m
y
= −1 and passes through (2, 5, −1).
a
Write the equation of P is point-slope form.
256
b
What is the z-intercept of P .
Q38
Given a plane with m
x
= 5 and m
y
= 2, we can conclude that the plane is steeper in the
x-direction than the y-direction. Is the x-direction the steepest direction we could travel in? If
not, what is?
4.1.10
Q39
Write the equation of a plane through (3, 0, 0), (0, 7, 0), and (0, 0, −1).
Q40
Write the equation of a plane with intercepts (2, 0, 0), (0, −2, 0), and (0, 0, 4).
Q41
Write the equation of a plane through (6, 4, 1), (6, 7, −2), and (8, 7, 1).
Q42
Write the equation of a plane through (2, 2, 1), (4, 2, 9), and (2, 0, 0).
Q43
Write the equation of a plane through (3, 4, 2), (5, 5, 6), and (7, 4, 6).
Q44
Write the equation of a plane through (1, 5, 2), (11, 5, 4), and (6, 3, −3).
4.1.11
Q45
Assuming you could draw in 4 dimensions, describe how you might construct the graph of x
2
1
+
x
2
3
+ x
2
4
= 25 in R
4
.
Q46
Assuming you could draw in 4 dimensions, describe how you might construct the graph of x
2
= x
2
3
in R
4
.
Q47
What equation(s) would describe the x
2
x
4
-plane in R
4
?
Q48
What would you call the object in R
4
defined by x
1
= 0?
257
Section 4.1
Exercises
Extension and Synthesis
Q49
The points (1, 0, 3) and (1, 4, 0) are both on the sphere S. What are the possible values for the
radius of S?
Q50
The graph of x
2
+ y
2
= 0 in R
2
is a point, not a curve. Use this idea to write an equation for the
intersection of the graphs f (x, y, z) = c and g(x, y, z) = d. What do you expect the dimension
of this intersection to be?
Q51
Suppose the x and y axes in R
2
were not perpendicular. Would the distance formula still hold?
Demonstrate.
258
Section 4.2
Functions of Several Variables
Goals:
1 Convert an implicit function to an explicit function.
2 Calculate the domain of a multivariable function.
3 Calculate level curves and cross sections.
If we want to understand the relationship between variables, a function is the gold standard. For
example, when we can write y as a function of x, then at each value of x, we simply need plug in
the value and simplify the arithmetic. There is no chance that algebraic manipulation will lead us to
multiple values of y, or to an equation we cannot solve. Naturally, we want to understand this type of
relationship between more than two variables. Much like our investigation of n-space, we’ll begin by
adding one variable. After this initial step, extrapolating to more variables will be straightforward.
Question 4.2.1
What Is a Function of More than One Variable?
Definition
A function of two variables is a rule that assigns a number (the output) to each ordered pair of real
numbers (x, y) in its domain. The output is denoted f(x, y).
Some functions can be defined algebraically. If f(x, y) =
p
36 − 4x
2
− y
2
then
f(1, 4) =
p
36 − 4 · 1
2
− 4
2
= 4.
Example 4.2.2
The Domain of a Function
Identify the domain of f(x, y) =
p
36 − 4x
2
− y
2
.
259
Example 4.2.2
The Domain of a Function
Solution
The only obstacle to evaluating this function is that the value under the square root might be negative.
We can write an inequality to express this and solve.
36 − 4x
2
− y
2
≥ 0
36 ≥ 4x
2
+ y
2
1 ≥
x
2
9
+
y
2
36
These are the points inside an ellipse whose intercepts are (±3, 0) and (0, ±6).
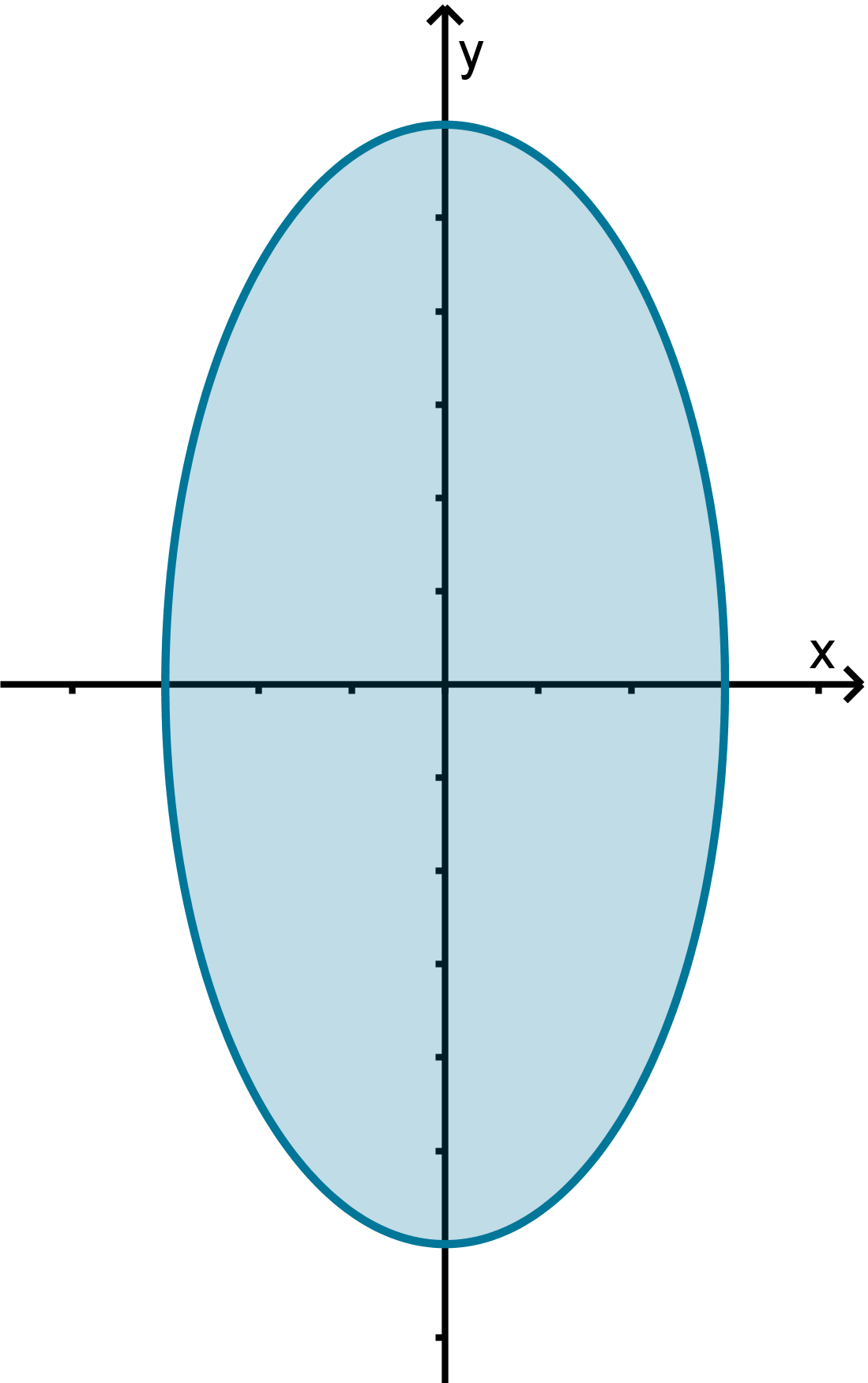
Figure: The domain of a function
Main Idea
When solving for the domain of an algebraic function, we look for the same obstacles to evaluating the
function that we do for one-variable functions.
Expressions in a denominator cannot be 0 (including built-in fractions like tan x =
sin x
cos x
)
Expressions in a square root must be greater than or equal to 0.
Expressions in a logarithm must be greater than 0.
The conditions these produce with a two-variable function may be harder to visualize or simplify than
with a function of one variable.
260
Application 4.2.3
Temperature Maps
Many useful functions cannot be defined algebraically. There is a function T (x, y) which gives
the temperature at each latitude and longitude (x, y) on earth. No pair (x, y) has more than one
temperature, and no pair fails to have a temperature. Still there is no hope of producing an expression
that computes T for any x and y. Mathematically (though perhaps not meteorologically) this function
is arbitrary.
T (−71.06, 42.36) = 50
T (−84.38, 33.75) = 59
T (−83.74, 42.28) = 41
Figure: A temperature map
This function is represented graphically by using color to portray the value of T at each point.
Application 4.2.4
Digital Images
A digital image is made up of pixels, each with a different color. In many modern images, these
pixels are too small to see. The color of each pixel is a function of that pixel’s location. Since colors are
harder to define numerically, we can consider the simpler case: where each pixel is a different shade of
gray. In this case we have a brightness function B(x, y) where the output is a number that represents
the brightness of the pixel at the coordinates (x, y).
y
x
687
1024
B(339, 773) = 158 B(340, 773) = 127
Figure: An image represented as a brightness function B on each pixel
261
Application 4.2.4
Digital Images
Remark
The brightness function differs from other functions we’ve studied in one key way. It is only defined for
(x, y) where x and y are integers. Other examples can take any real numbers as coordinates. This makes
our usual calculus methods impossible. We cannot get arbitrarily close to a point in order to compute a
limit. All other points are at least 1 unit away. However, if we are willing to settle for approximations,
we can apply calculus and get useful results.
Question 4.2.5
What Is the Graph of a Two-Variable Function?
A graph is our most important way to visualize a function. The graph of a one variable functions
is an object in two-space. One dimension measures the input variable. The other measures the output.
For a two variable function, the graph lies in three-space.
Definition
The graph of a function f(x, y) is the set of all points (x, y, z) that satisfy
z = f (x, y).
The height z above a point (x, y) represents the value of the function at (x, y). In this figure,
f(1, 4) is equal to the height of the graph above (1, 4, 0).
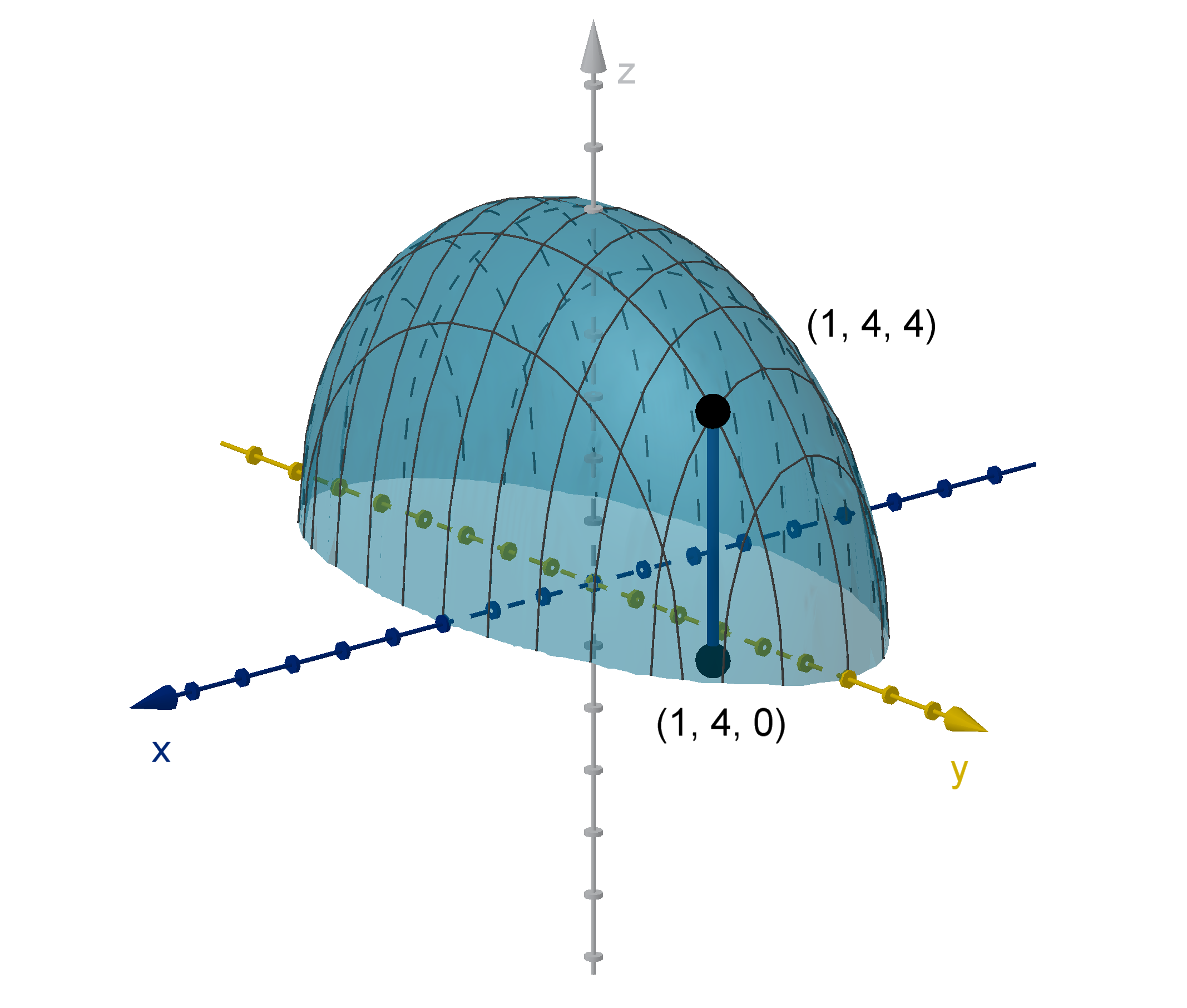
Figure: The graph z =
p
36 − 4x
2
− y
2
262
Question 4.2.6
How Do We Visualize a Graph in Three-Space?
Three-space is harder to visualize than two-space. What’s more, plotting points is more arduous with
two dimensions of inputs. In the absence of computer graphics, mathematicians have used a variety of
visualization tools.
Definition
A level set of a function f(x, y) is the graph of the equation f(x, y) = c for some constant c. For a
function of two variables this graph lies in the xy-plane and is called a level curve.
Example
Consider the function
f(x, y) =
p
36 − 4x
2
− y
2
.
The level curve
p
36 − 4x
2
− y
2
= 4 simplifies to 4x
2
+ y
2
= 20.
This is an ellipse.
Other level curves have the form
p
36 − 4x
2
− y
2
= c or 4x
2
+y
2
=
36 − c
2
. These are larger or smaller ellipses.
Level curves take their shape from the intersection of z = f(x, y) and z = c. Seeing many level
curves at once can help us visualize the shape of the graph.
Figure: The graph z = f (x, y), the planes z = c, and the level curves
263
Example 4.2.7
Drawing Level Curves
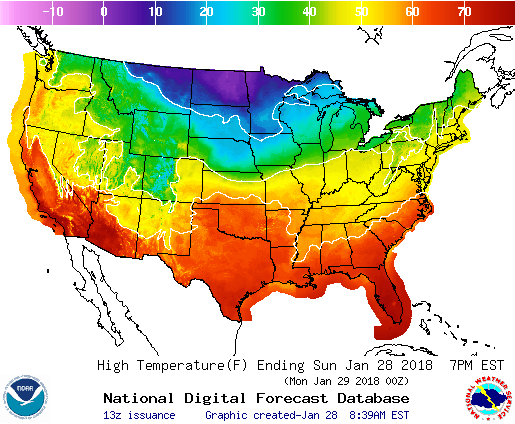
Where are the level curves on this temperature map?
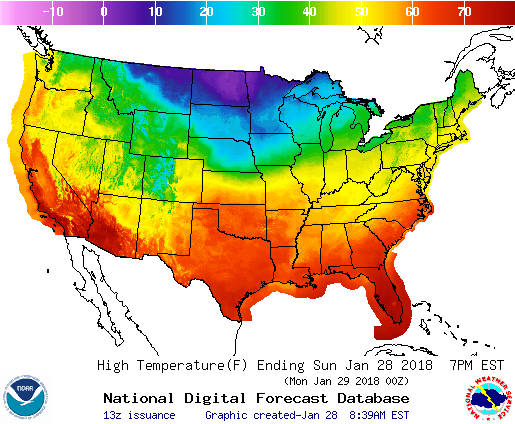
Figure: A temperature map
Solution
The level sets are the points where the temperature has a certain value. Since the colors represent ranges
of temperatures, it’s difficult to pick out the level sets within that range. However, at the transition from
one color to the next, we know that the temperature is equal to the cutoff temperature between those
ranges. The picture below shows a reasonable attempt to sketch three level curves in white. Notice
that the level curves (especially the one between green and yellow) are not connected, and that drawing
them in perfect detail is beyond the ability of a human.
264
Example 4.2.8
Using Level Curves to Describe a Graph
What features can we discern from the level curves of this topographical map?
Figure: A topographical map
265
Example 4.2.8
Using Level Curves to Describe a Graph
Solution
A
B
C
D
D
D
There are many features we could describe. Here is a sample.
The point A is surrounded by relatively flat terrain. There are not many level curves here, which
means the altitude is not increasing or decreasing to higher or lower levels.
The points B and C are on slopes. If we travel north and south we cross level curves, meaning
our altitude is increasing or decreasing. The slope is steeper at B than at C, because traveling
north from B we cross more level curves than traveling north from C
The points marked D are in the middle of a series of rings of level curves. These are either the
tops of hills or (less likely given the context) the bottoms of valleys.
Example 4.2.9
A Cross Section
Definition
The intersection of a plane with a graph is a cross section. A level curve is a type of cross section, but
not all cross sections are level curves.
266
Find the cross section of z =
p
36 − 4x
2
− y
2
at the plane y = 1.

Figure: The y = 1 cross section of z =
p
36 − 4x
2
− y
2
Example 4.2.10
Converting an Implicit Equation to a Function
Definition
We sometimes call an equation in x, y and z an implicit equation. Often in order to graph these, we
convert them to explicit functions of the form z = f(x, y)
Write the equation of a paraboloid x
2
− y + z
2
= 0 as one or more explicit functions so it can be
graphed. Then find the level curves.

Figure: Level curves of x
2
− y + z
2
= 0
267
Question 4.2.11
How Does this Apply to Functions of More Variables?
We can define functions of three variables as well. Denoting them f(x, y, z). For even more variables,
we use x
1
through x
n
. The definitions of this section can be extrapolated as follows.
Variables 2 3 n
Function f(x, y) f(x, y, z) f(x
1
, . . . , x
n
)
Domain subset of R
2
subset of R
3
subset of R
n
Graph z = f (x, y) in R
3
w = f(x, y, z) in R
4
x
n+1
= f(x
1
, . . . , x
n
) in R
n+1
Level Sets level curve in R
2
level surface in R
3
level set in R
n
Observation
We might hope to solve an implicit equation of n variables to obtain an explicit function of n − 1
variables. However, we can also treat it as a level set of an explicit function of n variables (whose graph
lives in n + 1 dimensional space).
x
2
+ y
2
+ z
2
= 25
F (x, y, z) = x
2
+ y
2
+ z
2
F (x, y, z) = 25
f(x, y) = ±
p
25 − x
2
− y
2
Both viewpoints will be useful in the future.
268
Section 4.2
Exercises
Summary Questions
Q1
What does the height of the graph z = f (x, y) represent?
Q2
What is the distinction between a level set and a cross section?
Q3
What are level sets in R
2
and R
3
called?
Q4
What is the difference between an implicit equation and explicit function?
4.2.1
Q5
If f(x, y) = 13x +
y
x
, compute f(2, −8).
Q6
If f(x, y) = cos(πxy), compute f
4,
1
3
.
Q7
Is f(x, y) = ±
√
4x − y a function? Explain.
Q8
Is the following a function? Explain.
f(x, y) =
(
√
y if y ≥ 0
√
x if x ≥ 0
269
Section 4.2
Exercises
4.2.2
Q9
Compute the domain of f(x, y) =
1
x+y
.
Q10
What is the domain of f(x, y) =
1
x
2
+y
2
?
Q11
What is the domain of g(x, y) = x
3
+
p
y
2
− 25?
Q12
What is the domain of g(x, y) = 15 + ln(y − 2x)?
Q13
What is the domain of f(x, y) =
√
x+3
y
2
−x
?
Q14
Compute the domain of h(x, y) =
4x
y−ln x
4.2.3
Q15
On the temperature map, we saw T (−84.38, 33.75) = 59. Is T (−84.38, 35.75) greater than or
less than 59?
Q16
On the temperature map, we saw T (−83.74, 42.28) = 41. Is T (−93.74, 42.28) greater than or
less than 41?
Q17
What range of temperatures are found in South Dakota? In which parts of the state are the
extreme temperatures found?
Q18
Can you use this diagram to approximate T (−61.06, 42.36)? Explain.
4.2.4
Q19
In our image of Mona Lisa, what is the domain of B?
Q20
In our blow-up of the digital image, we see Mona Lisa’s eye is near the coordiante (369, 800).
Where is her other eye?
270
4.2.5
Q21
Can the points (1, 3, 5) and (1, 3, 7) both be on the graph of z = f(x, y)? Explain.
Q22
If the graph z = f (x, y) is below the xy-plane, what does that tell us about f (x, y)?
Q23
If f(x, y) has a z-intercept of c, what does that tell us about f?
Q24
What is the significance of the points where the graph z = f (x, y) intersects the xy-plane?
4.2.6
Q25
Describe the level curves of f(x, y) = (x − 2)
2
+ (y + 1)
2
.
Q26
Describe the level curves of f(x, y) = x
2
− 3y + 5.
Q27
Describe the level curves of
x
2
y
.
Q28
Describe the level curves of g(x, y) =
y
e
x
.
Q29
Give the equation of the level curve of f(x, y) = x
3
+ y
3
that passes through (4, 2).
Q30
Give the equation of the level curve of g(x, y) = 17x
2
−3xy + y
3
that contains the point (1, 2).
Q31
Given a function f(x, y), how many level curves might pass through (3, 7)?
Q32
If the points (x
1
, y
1
) and (x
2
, y
2
) lie on the same level curve of h(x, y), what are the possible
values of the expression h((x
1
, y
1
) − h(x
2
, y
2
)?
271
Section 4.2
Exercises
4.2.7
Q33
In our level curves on the temperature map, what physical meaning can we take from the fact
that the green-yellow and red-orange level curves are closer together in Kansas than they are
farther east?
Q34
Explain why it makes sense physically that level curves of a temperature function would be
complicated and disconnected.
4.2.8
Q35
In the topographical map, what can we deduce from the fact that no level curves cross the farm
fields in the lower center of the map?
Q36
Explain why it makes physical sense that there are level curves alongside the creeks in this map.
4.2.9
Q37
Give an equation for the y = 2 cross-section of the graph z = f(x, y) where f(x, y) = x
3
+ y
3
.
Q38
Consider the plane P whose equation is f(x, y) = 3x − 5y + 7.
i. Give the equation of the y = 0 cross section of P . What is this graph? What is the
significance of the various parts of its equation?
ii. Give the equation of the x = 0 cross section of P . What is the significance of the various
parts of its equation?
iii. Give the equation and describe the set of all level curves of f.
Q39
If the cross sections of z = f (x, y) in the planes y = b are identical for all values of b, what does
that tell us about f?
Q40
If f(x, y) is a function that satisfies f(x, y) = f (x, −y) for all x and y, how will this be refelected
in the cross sections of z = f (x, y)?
272
4.2.10
Q41
Rewrite y = x
2
+ z
2
as one or more explicit functions z = f (x, y).
Q42
Rewrite ln x + ln y + ln z = 0 as one or more explicit functions z = f(x, y).
Q43
Rewrite x
2
+ y
2
+ z
2
+ xyz = 20 as one or more explicit functions z = f(x, y).
Q44
Explain why it would be difficult to write
ln y
z
−
√
xz = 5 + x as an explicit function of the form
z = f (x, z). Choose a better dependent and variable and write that variable as a function of the
other two.
4.2.11
Q45
Consider the function f(x
1
, x
2
, x
3
, x
4
, x
5
).
a
What space does the graph of f lie in?
b
What space does a level set of f lie in?
Q46
Write xyz = 1 as
a
A level set of a function
b
An explicit function z = f (x, y)
Q47
Consider a one-variable function f (x).
a
What space does the graph of f(x) lie in?
b
Where does a level set of f lie in? What does a typical level set look like?
Q48
Show how the graph of an explicit function x
n+1
= f(x
1
, x
2
, . . . , x
n
) can be converted to the
level set of an n + 1-variable function.
273
Section 4.2
Exercises
Synthesis & Extension
Q49
Let f(x, y) = x
2
. Sketch the graph of z = f(x, y). What is the role of y in this graph?
Q50
Consider the implicit equation zx = y
a
Rewrite this equation as an explicit function z = f (x, y).
b
What is the domain of f?
c
Solve for and sketch a few level sets of f.
d
What do the level sets tell you about the graph z = f (x, y)?
Q51
Consider the implicit equation: x = sin z.
a
Sketch a graph of the equation.
b
Describe (in words) what the cross section of the graph in the x =
1
2
plane looks like.
274
Section 4.3
Limits and Continuity
Goals:
1 Understand the definition of a limit of a multivariable function.
2 Use the Squeeze Theorem
3 Apply the definition of continuity.
Limits of multivariable functions are conceptually similar to one-variable functions. However, even
though the requirement is the same, it is a much harder to satisfy. Since there are so many more ways
to approach a given point in a higher dimensional space, there are more nearby points to check to see
whether the function is actually approaching the proposed limit.
Question 4.3.1
What Is the Limit of a Function?
Definition
We write
lim
(x,y)→(a,b)
f(x, y) = L
if we can make the values of f stay arbitrarily close to L by restricting to a sufficiently small neighborhood
of (a, b).
Proving a limit exists requires a formula or rule. For any amount of closeness required (ϵ), you must
be able to produce a radius δ around (a, b) sufficiently small to keep |f(x, y) −L| < ϵ. For this reason,
we will not prove that any limits exist. We will present three examples of functions whose limit does
not exist.
Example 4.3.2
A Limit That Does Not Exist
Show that lim
(x,y)→(0,0)
x
2
− y
2
x
2
+ y
2
does not exist.
275
Example 4.3.2
A Limit That Does Not Exist
Solution
Let’s define f(x, y) =
x
2
−y
2
x
2
+y
2
. We will approach the point (0, 0) from two different directions. If
we approach along the x-axis, then the points on our path have the form (x, 0). When we plug these
into the function, the value is f(x, 0) =
x
2
−0
x
2
+0
. This is equal to 1 for all values of x except 0, so as x
approaches 0, the values of f are arbitrarily close (in fact exactly equal) to 1.
On the other hand, if we approach 1 along the y-axis, then the points have the form (0, y). When
we plug these into the function, the value is f(0, y) =
0−y
2
0+y
2
. This is equal to −1 for all values of y
except 0, so as y approaches 0, the values of f are arbitrarily close (in fact exactly equal) to −1.
What does this say about the limit of f ? The lim
(x,y)→(0,0)
f(x, y) = 1 because there are points on the
y-axis do not give values close to 1, but any neighborhood of (0, 0) includes some points on the y-axis.
Similarly, lim
(x,y)→(0,0)
f(x, y) = −1. If we tried to argue that the limit had any other value, the x-axis
and y-axis would both present a problem. This this limit does not exist.
We can identify the problem behavior in the graph of z = f(x, y). As the graph approaches the
origin, there are points of all heights between −1 and 1. Specifically we can see the line above the x-axis
and below the y-axis. No amount of closeness can exclude this range of values.
Figure: A function with no limit at (0, 0)
We might take away the idea that checking limits of two-variable functions requires checking in both
the x-direction and the y-direction. Unfortunately, even that is not sufficient.
Example 4.3.3
Another Limit That Does Not Exist
Show that lim
(x,y)→(0,0)
xy
x
2
+ y
2
does not exist.
276
Solution
Let f(x, y) =
xy
x
2
+y
2
. We can check the values of this function on the x- and y-axes. Except at (0, 0),
f(x, 0) = 0 and f(0, y) = 0. However, not all the points close to (0, 0) lie on an axis. Suppose we work
with the points on another line: y = mx. These points have the form (x, mx). We can evaluate f on
this line.
f(x, xm) =
(x)(mx)
x
2
+ (mx)
2
=
mx
2
(m
2
+ 1)x
2
=
m
m
2
+ 1
(except at (0, 0))
Thus there are point arbitrarily close to (0, 0) on which f is valued as low as −0.5 (m = −1) and as
high as 0.5 (m = 1). The limit does not exist.
Figure: The graph z =
xy
x
2
+y
2
and the line of height
1
2
over x = y.
We might take away the idea that checking limits of two-variable functions requires checking along
each line through the point in question. Unfortunately, even that is not sufficient.
Example 4.3.4
Yet Another Limit That Does Not Exist
Show that lim
(x,y)→(0,0)
xy
2
x
2
+ y
4
does not exist.
Solution
Let f(x, y) =
xy
2
x
2
+y
4
. We can check the values of this function on the x- and y-axes. Except at (0, 0),
277
Example 4.3.4
Yet Another Limit That Does Not Exist
f(x, 0) = 0 and f(0, y) = 0. We can also check the values along a line of the form y = mx.
f(x, xm) =
(x)(mx)
2
x
2
+ (mx)
4
=
m
2
x
3
x
2
(1 + m
4
x
2
)
lim
x→0
f(x, xm) = lim
x→0
m
2
x
3
x
2
(1 + m
4
x
2
)
= lim
x→0
m
2
x
1 + m
4
x
2
= 0
Thus along each line, the values of f approach 0 as we approach the origin. However, we have not
considered paths that are not line. Consider the parabola x = y
2
. Points on this parabola have the form
(y
2
, y). We compute the values on this parabola.
f(y
2
, y) =
(y
2
)(y)
2
(y
2
)
2
+ y
4
=
y
4
2y
4
For any point on this parabola except the origin f has a value of
1
2
. Thus f takes values of
1
2
and 0 in
any neighborhood of (0, 0), meaning the limit does not exist.
Figure: The graph z =
xy
2
x
2
+y
4
, which limits to 0 along any line through the origin, but has height
1
2
over the parabola x = y
2
We take away from these exercises that establishing the value of a multi-variable limit cannot be
reduced to computing a single-variable limit, or even a family of single-variable limits. The formal
arguments that establish multi-variable limits are more advanced and beyond the scope of this text.
278
Question 4.3.5
What Tools Apply to Multi-Variable Limits?
The limit laws from single-variable limits transfer comfortably to multi-variable functions.
1 Sum/Difference Rule
2 Constant Multiple Rule
3 Product/Quotient Rule
These rules allow us to compute limits of complicated functions from simpler ones. How do we come
by those simpler limits in the first place? We can apply the kind of advanced arguments we alluded to
earlier. Another tool is the squeeze theorem.
The Squeeze Theorem
If g < f < h in some neighborhood of (a, b) and
lim
(x,y)→(a,b)
g(x, y) = lim
(x,y)→(a,b)
h(x, y) = L,
then
lim
(x,y)→(a,b)
f(x, y) = L.
Question 4.3.6
What Is a Continuous Function?
Definition
We say f(x, y) is continuous at (a, b) if
lim
(x,y)→(a,b)
f(x, y) = f(a, b).
In a rigorous development of calculus, we compute limits and use them to show that functions are
continuous. Given that evaluating limits is beyond our current means, we will reverse the process. Rather
than worrying about how to prove the following theorem, we will assume it is true and use it to evaluate
limits.
279
Question 4.3.6
What Is a Continuous Function?
Theorem
Polynomials, roots, trig functions, exponential functions and logarithms are continuous on their
domains.
Sums, differences, products, quotients and compositions of continuous functions are continuous
on their domains.
The limit of a continuous function is equal to the value of the function. When we need to compute
a limit of these functions, we’ll just evaluate them instead. Why didn’t this work in our examples? In
each of our examples, the function was a quotient of polynomials, but (0, 0) was not in the domain.
Remark
Limits, continuity and these theorems can all be extrapolated to functions of more variables.
Section 4.3
Exercises
Summary Questions
Q1
Why is it harder to verify a limit of a multivariable function?
Q2
What do you need to check in order to determine whether a function is continuous?
280
Section 4.4
Partial Derivatives
Goals:
1 Calculate partial derivatives.
2 Realize when not to calculate partial derivatives.
The first task in developing calculus is to understand rates of change. In the single-variable case, we
ask how the dependent variable changes per unit of increase in the independent variable. With more
than one independent variable we must ask: what kind of increase do we mean? There is more than
one possible answer. Partial derivatives are the simplest and most intuitive rate of change.
Question 4.4.1
What Is the Rate of Change of a Multivariable Function?
Motivational Example
The force due to gravity between two objects depends on their masses and on the distance between
them. Suppose at a distance of 8, 000km the force between two particular objects is 100 newtons and
at a distance of 10, 000km, the force is 64 newtons.
How much do we expect the force between these objects to increase or decrease per kilometer of
distance?
Solution
The change in force divided by the change in distance is
64N −100N
10, 000km − 8, 000km
= −0.018
N
km
Notice that the change in force is entirely attributable to the change in distance. That is because the
masses of the objects did not change. The only change in the dependent variables is the 2, 000km
increase in distance.
Our goals in understanding multi-variable rates of change are guided by what we accomplished with
one variable. Derivatives of a single-variable function were a way of measuring the change in a function.
Recall the following facts about f
′
(x).
1 Average rate of change is realized as the slope of a secant line:
f(x) − f (x
0
)
x − x
0
281
Question 4.4.1
What Is the Rate of Change of a Multivariable Function?
2 The derivative f
′
(x) is defined as a limit of slopes:
f
′
(x) = lim
h→0
f(x + h) − f (x)
h
3 The derivative is the instantaneous rate of change of f at x.
4 The derivative f
′
(x
0
) is realized geometrically as the slope of the tangent line to y = f(x) at x
0
.
5 The equation of that tangent line can be written in point-slope form:
y −y
0
= f
′
(x
0
)(x − x
0
)
In the physics example above, the rate of change was easier to understand because only one inde-
pendent variable is changing. That was an average rate of change, taken between two points. We now
develop a corresponding instantaneous rate of change. A partial derivative measures the rate of change
of a multivariable function as one variable changes, but the others remain constant.
Definition
The partial derivatives of a two-variable function f(x, y) are the functions
f
x
(x, y) = lim
h→0
f(x + h, y) − f(x, y)
h
and
f
y
(x, y) = lim
h→0
f(x, y + h) − f (x, y)
h
.
We can see the idea of each partial derivative in the formula. f
x
compares the values of f at
(x + h, y) and (x, y). The x values change between these two points, but the y values remain constant.
The opposite is true in the formula for f
y
.
Notation
The partial derivative of a function can be denoted a variety of ways. Here are some equivalent notations
f
x
∂f
∂x
∂z
∂x
∂
∂x
f
D
x
f
282
Example 4.4.2
Computing a Partial Derivative
Find
∂
∂y
(y
2
− x
2
+ 3x sin y).
Main Idea
To compute a partial derivative f
y
, perform single-variable differentiation. Treat y as the independent
variable and x as a constant.
Solution
We take an ordinary derivative, treating y as the variable and x as a constant. The familiar rules of
derivatives apply. The sum rule means we can differentiate term-by-term.
∂
∂y
y
2
= 2y
∂
∂y
x
2
= 0, since the x
2
term is treated as constant.
∂
∂y
3x sin y = 3x cos y, since 3x is treated as constant multiple of the function sin y.
Together this gives the partial derivative
∂
∂y
(y
2
− x
2
+ 3x sin y) = 2y + 3x cos y.
Synthesis 4.4.3
Interpreting Derivatives from Level Sets
Below are the level curves f(x, y) = c for some values of c. Can we tell whether f
x
(−4, 1.25) and
f
y
(−4, 1.25) are positive or negative?
283
Synthesis 4.4.3
Interpreting Derivatives from Level Sets
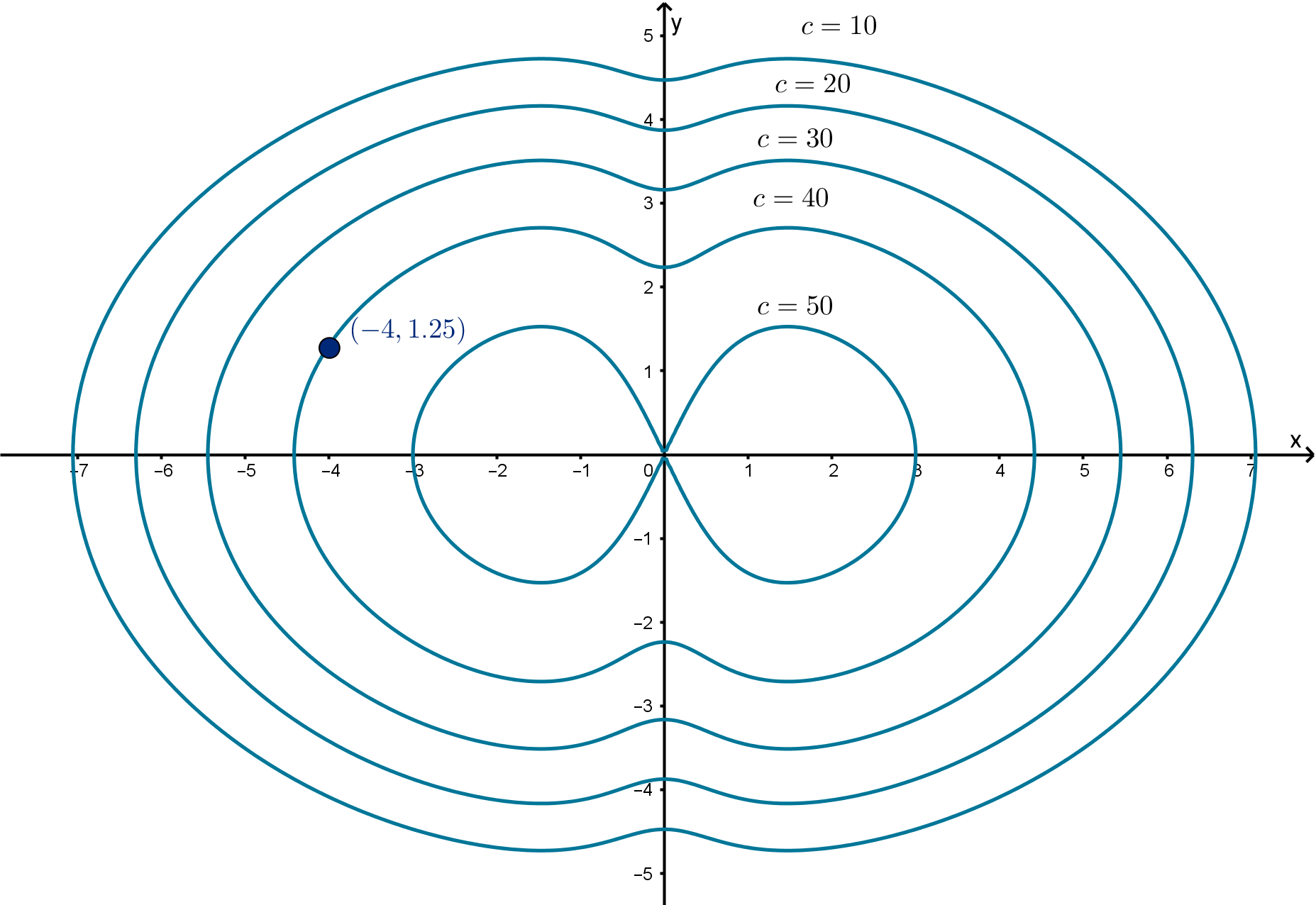
Figure: Some level curves of f(x, y)
Solution
As x increases and y remains constant, we travel to the right in the coordinate plane. Based on the
labeling of the level curves, this takes f from the value 40 to values between 40 and 50, meaning f
increases. Thus f
x
> 0.
Similarly, as y increases and x remains constant, we travel upwards in the coordinate plane. This
takes f from the value 40 to values between 30 and 40, meaning f decreases. Thus f
y
< 0.
Question 4.4.4
What Is the Geometric Significance of a Partial Derivative?
The partial derivative f
x
(x
0
, y
0
) is realized geometrically as the slope of the line tangent to z =
f(x, y) at (x
0
, y
0
, z
0
) and traveling in the x direction. Since y is held constant, this tangent line lives in
y = y
0
, a plane perpendicular to the y-axis. The line is tangent to the cross section of the graph with
that plane.
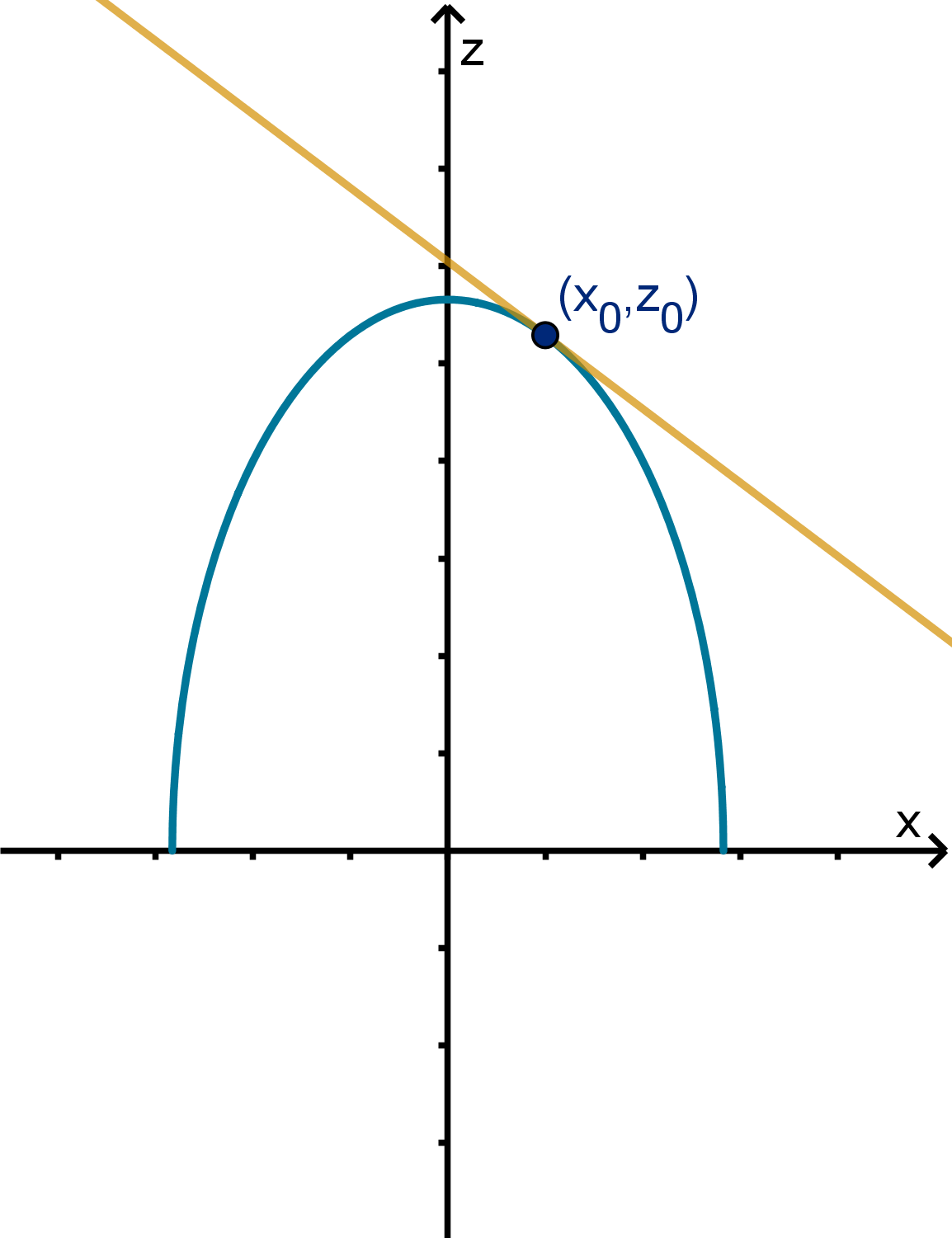
Figure: The tangent line to z = f (x, y) in the x direction
284
Example 4.4.5
Derivative Rules and Partial Derivatives
Find f
x
for the following functions f(x, y):
a
f =
√
xy (on the domain x > 0, y > 0)
b
f =
y
x
c
f =
√
x + y
d
f = sin (xy)
Solution
a
We can rewrite this as f (x, y) =
√
x
√
y. In this setting,
√
y is a constant multiple. Thus
f
x
(x, y) =
1
2
√
x
√
y
b
We can rewrite this as f (x, y) =
1
x
y. We treat y as a constant multiple. f
x
(x, y) = −
1
x
2
y.
c
We cannot rewrite this as f (x, y)
√
x +
√
y, because that is not a valid algebraic manipulation.
Instead we use the chain rule.
The outer function is
√
x. Its derivative is
1
2
√
x
.
The inner function is x + y. Its derivative is 1.
By the chain rule
∂
∂x
√
x + y =
1
2
√
x + y
(1) =
1
2
√
x + y
d
We do not have an easy trig rule to break up products. We’ll use the chain rule again.
The outer function is sin x. Its derivative is cos x.
The inner function is xy. Its derivative is y.
By the chain rule
∂
∂x
sin(xy) = cos(xy)y
Main Idea
Sometimes we can detach the variable held constant from the changing variable using the rules of
algebra. When we can’t, we’ll often need a differentiation rule (usually the chain rule).
285
Question 4.4.6
What If We Have More than Two Variables?
We can also calculate partial derivatives of functions of more variables. All variables but one are
held to be constants. :
Example
If
f(x, y, z) = x
2
− xy + cos(yz) − 5z
3
,
then
∂f
∂y
= 0 − x − sin(yz)z − 0
= −x − z sin(yz)
Example 4.4.7
A Function of Three Variables
For an ideal gas, we have the law P =
nRT
V
, where P is pressure, n is the number of moles of gas
molecules, T is the temperature, and V is the volume.
a
Calculate
∂P
∂V
.
b
Calculate
∂P
∂T
.
c
(Science Question) Suppose we’re heating a sealed gas contained in a glass container. Does
∂P
∂T
tell us how quickly the pressure is increasing per degree of temperature increase?
Solution
a
We can write P = nrT
1
V
and treat nrT as a constant multiple. Then
∂P
∂V
= nrT
−
1
V
2
.
b
In this case, nr
1
V
is a constant multiple.
∂P
∂T
= nr
1
V
(1).
c
No.
∂P
∂T
assumes n and V are constant, but glass expands as it heats. The volume of both the
container and the gas is increasing, not constant.
286
Question 4.4.8
How Do Higher Order Derivatives Work?
Taking a partial derivative of a partial derivative gives us a higher order partial derivative. We use
the following notation.
Notation
(f
x
)
x
= f
xx
=
∂
2
f
∂x
2
We need not use the same variable each time
Notation
(f
x
)
y
= f
xy
=
∂
∂y
∂
∂x
f =
∂
2
f
∂y∂x
Remark
Notice the subscript notation and the ∂ notation express higher order derivatives in opposite order.
Subscripts are added to the right of f, which the differential operation is applied on the left of f.
Example 4.4.9
A Higher Order Partial Derivative
If f(x, y) = sin(3x + x
2
y) calculate f
xy
.
287
Example 4.4.9
A Higher Order Partial Derivative
Solution
First we compute f
x
. We’ll need the chain rule.
The outer function is sin x. Its derivative is cos x.
The inner function is 3x + x
2
y. Its derivative is 3 + 2xy.
f
x
= cos(3x + x
2
y)(3 + 2xy).
Computing (f
x
)
y
will require the product rule.
∂
∂y
cos(3x + x
2
y) requires the chain rule.
The outer function is cos x. Its derivative is −sin x.
The inner function is 3x + x
2
y. Its derivative is x
2
.
∂
∂y
cos(3x + x
2
y) = −sin(3x + x
2
y)(x
2
).
Now we apply the product rule.
∂
∂y
cos(3x + x
2
y)(3 + 2xy) =
∂
∂y
cos(3x + x
2
y)
(3 + 2xy) + cos(3x + x
2
y)
∂
∂y
(3 + 2xy)
= −sin(3x + x
2
y)(x
2
)(3 + 2xy) + cos(3x + x
2
y)(2x)
Question 4.4.10
Does Differentiation Order Matter?
No. Specifically, the following is due to Clairaut:
Theorem
If f is defined on a neighborhood of (a, b) and the functions f
xy
and f
yx
are both continuous on that
neighborhood, then f
xy
(a, b) = f
yx
(a, b).
This readily generalizes to larger numbers of variables, and higher order derivatives. For example
f
xyyz
= f
zyxy
.
288
Section 4.4
Exercises
Summary Questions
Q1
What is the role of each variable when we compute a partial derivative?
Q2
What does the partial derivative f
y
(a, b) mean geometrically?
Q3
Can you think of an example where the partial derivative does not accurately model the change
in a function?
Q4
What is Clairaut’s Theorem?
4.4.1
Q5
Give the equation of the line that lies in the plane x = 2 and is tangent to the graph z = xe
3xy
+x
at the point (2, 0, 4). You may give your equation in any notation that works in 2 dimensions.
Q6
Alexander performs an experiment with his wireless networking router. At each level of power
output (in miliwatts) and distance from his computer (in meters), he measures T (p, d), the
maximum transfer speed of data (in megabits per second). Here is a table of his observations.
0mW 100mW 200mW 300mW 400mW 500mW 600mW 700mW
10m 6 15 40 100 300 800 800 800
20m 0 2 15 30 90 300 800 800
30m 0 0 2 10 50 100 400 800
40m 0 0 0 0 5 20 50 100
50m 0 0 0 0 2 5 20 45
a
Use this data to approximate T
p
(300, 20). Show what values you used. There is more than
one reasonable way to do this.
b
What does the derivative in
a
mean in physical terms? Be precise and include units.
289
Section 4.4
Exercises
c
Use this data to approximate T
d
(500, 30). Show what values you used. There is more than
one reasonable way to do this.
d
What appears to be true about the sign of T
d
(p, d)? What does this mean in physical terms,
and why does it make sense?
4.4.2
Q7
Let f(x, y) = 7x
2
+ 5y cos x + e
y
. Compute f
x
(x, y). Explain the role of y in each term where
it is present.
Q8
Let f(x, y) = sin x sin y. Show how to compute f
y
(x, y) using the product rule, then suggest a
more efficient approach.
4.4.3
Q9
In the diagram from this example, is f
x
(3, 0) positive or negative? Explain.

Q10
In the diagram from this example, use a point on the c = 30 level set to approximate f
y
(4, −1.25).
290
Q11
In the diagram from this example, use a point on the c = 50 level set to approximate f
x
(4, −1.25).
Q12
In the diagram from this example, what is f
y
(0, 0)? Explain your reasoning.
4.4.4
Q13
Find f
x
and f
y
for the following functions f(x, y)
a
f(x, y) = x
2
− y
2
b
f(x, y) =
p
y
x
(assume x > 0 and y > 0)
c
f(x, y) = ye
xy
Q14
Find g
x
(x, y) and g
y
(x, y) for the following functions g(x, y)
a
g(x, y) = e
x
2
+y
2
b
g(x, y) = y ln(y −x)
c
g(x, y) =
3x
2
+4x−2
e
(y
3
)
4.4.5
Q15
Extrapolate from the limit defintion of f
x
(x, y) to give a limit definition of f
x
(x, y, z). Explain
why this limit represents a change in f where only x is changing.
Q16
Let f(x, y, z) = e
3x
y +
3
√
yz + x
3
z
7
. Compute
∂f
∂z
.
Q17
Let g(u, v, w) = e
uv+w
2
. Compute
∂g
∂v
.
Q18
Let p(r, s, t) =
e
r
+e
s
+e
t
rst
. Compute
∂p
∂r
.
291
Section 4.4
Exercises
4.4.6
Q19
In this example, does the fact that glass expands as it is heated suggest that
∂P
∂T
overstates or
understates the actual rate of pressure increase as T increases?
Q20
Suppose Jinteki Corporation makes widgets which is sells for $100 each. It commands a small
enough portion of the market that its production level does not affect the demand (price) for its
products. If W is the number of widgets produced and C is their operating cost, Jinteki’s profit
is modeled by
P = 100W − C.
Since
∂P
∂W
= 100 does this mean that increasing production can be expected to increase profit at
a rate of $100 per widget?
4.4.7
Q21
Suppose g(s, t) is the partial derivative of f (s, t) with respect to t, and h(s, t) is the partial
derivative for g(s, t) with respect to s. Write h in terms of f using both subscript and ∂
notation.
Q22
Physicists note that velocity is the derivative of position with respect to time, and acceleration
is the derivative of velocity with respect to time. If s(t, f) is the position of a rocket with f
kilograms of fuel after t seconds, what is the physical meaning of
∂
3
s
∂
2
t∂f
?
4.4.8
Q23
If f (x, y) = sin(3x + x
2
y) calculate f
yx
. Verify that you get the same answer that we did for
f
xy
.
Q24
Let f(x, y) = ln(x
2
+ y). Compute f
xy
(x, y).
Q25
Let g(x, y, z) = 2x
3
z + ye
xy
2
.
a
Compute
∂g
∂y
.
292
b
Compute
∂
2
g
∂x
2
.
Q26
Compute the following partial derivatives of
g(x, y, z) =
x
3
sin(xz)
y
a
∂g
∂y
b
∂
2
g
∂z
2
c
∂
2
g
∂z∂x
4.4.9
Q27
If f(x, y, z) is a smooth function, which of the following are equavalent to f
xyyzy
?
i. f
xzzyz
ii. f
zyyxy
iii. f
yyyzx
iv. f
xxxyz
v. f
xyzy
vi. f
xyz
vii. f
yxxzx
Q28
How many third partial derivatives does a two-variable function have? Assuming these derivatives
are continuous, which of them are equal according to Clairaut’s theorem?
293
Section 4.4
Exercises
Synthesis & Extension
Q29
Let f(x, y) =
e
xy
x+y
. Is
∂f
∂x
=
∂f
∂y
? If so, why? If not, how are they related?
Q30
The function f (x, y) = e
x+y
has the strange property that f
x
x, y = f
y
(x, y) at every point
(x, y). What does this mean geometrically about the function f?
Q31
Do we know that f
x
(x, y) is in fact a function? What fact about limits is relevant to this
question?
294
Section 4.5
Linear Approximations
Goals:
1 Calculate the equation of a tangent plane.
2 Rewrite the tangent plane formula as a linearization or differential.
3 Use linearizations to estimate values of a function.
4 Use a differential to estimate the error in a calculation.
In single-variable calculus, the tangent line was one of the great applications of the derivative. It
solves a difficult geometry problem, but it also gives a method of approximating a difficult to compute
function. The height of the tangent line is close to the height of the graph near the point of tangency.
This means the value of the tangent line function approximates the value of the function, close to the
point of tangency. The two-variable analogue of a tangent line is a tangent plane.
Question 4.5.1
What Is a Tangent Plane?
Definition
A tangent plane at a point P = (x
0
, y
0
, z
0
) on a surface is a plane containing the tangent lines to the
surface through P .
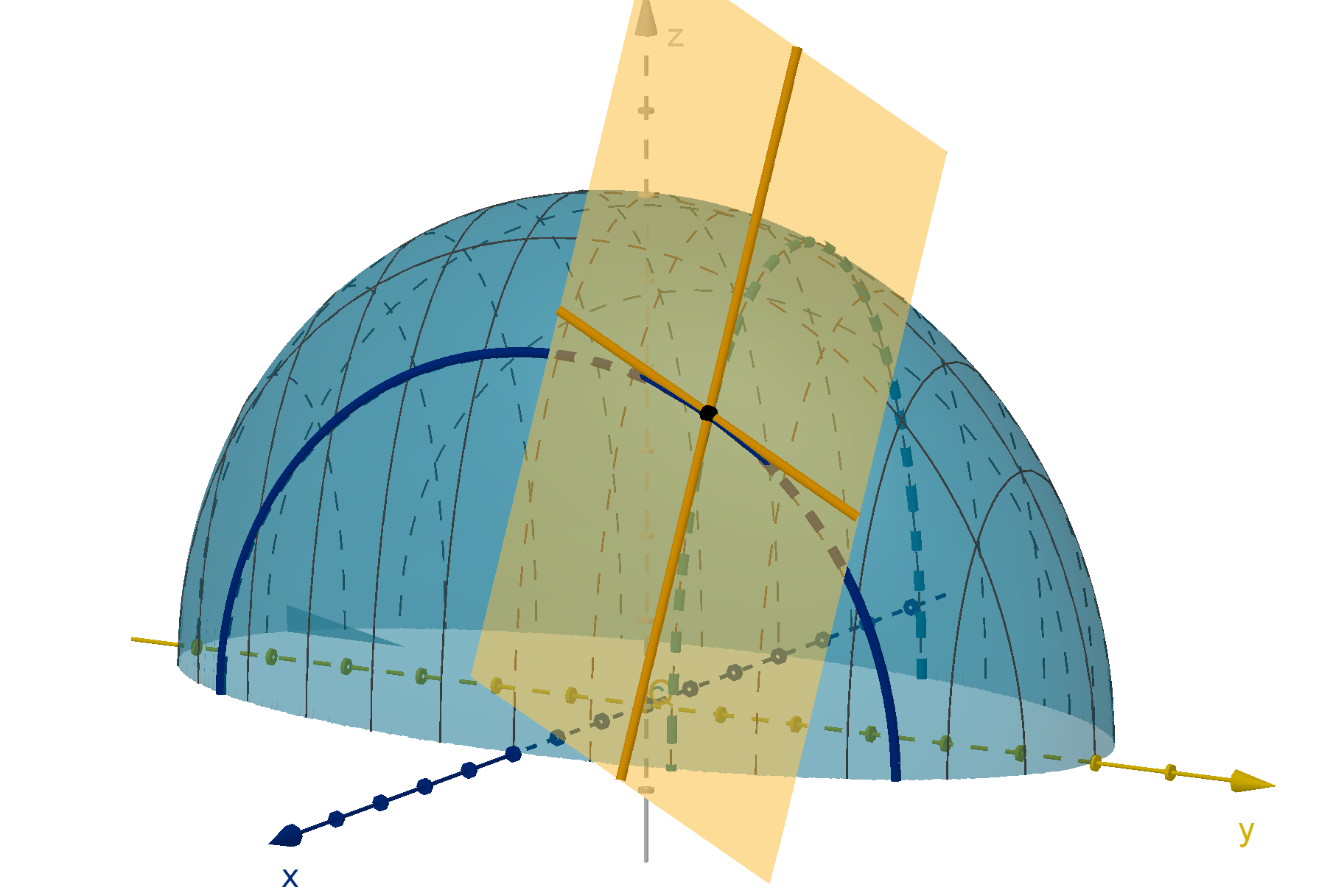
Figure: The tangent plane to z = f (x, y) at a point
295
Question 4.5.1
What Is a Tangent Plane?
Equation
If the graph z = f (x, y) has a tangent plane at (x
0
, y
0
), then it has the equation:
z − z
0
= f
x
(x
0
, y
0
)(x − x
0
) + f
y
(x
0
, y
0
)(y −y
0
).
Remarks
1 This is the point-slope form of the equation of a plane. f
x
(x
0
, y
0
) and f
y
(x
0
, y
0
) are the slopes.
2 x
0
and y
0
are numbers, so f
x
(x
0
, y
0
) and f
y
(x
0
, y
0
) are numbers. The variables in this equation
are x, y and z.
The cross sections of the tangent plane give the equation of the tangent lines we learned in single
variable calculus.
y = y
0
x = x
0
z − z
0
= f
x
(x
0
, y
0
)(x − x
0
) + 0 z − z
0
= 0 + f
y
(x
0
, y
0
)(y −y
0
)
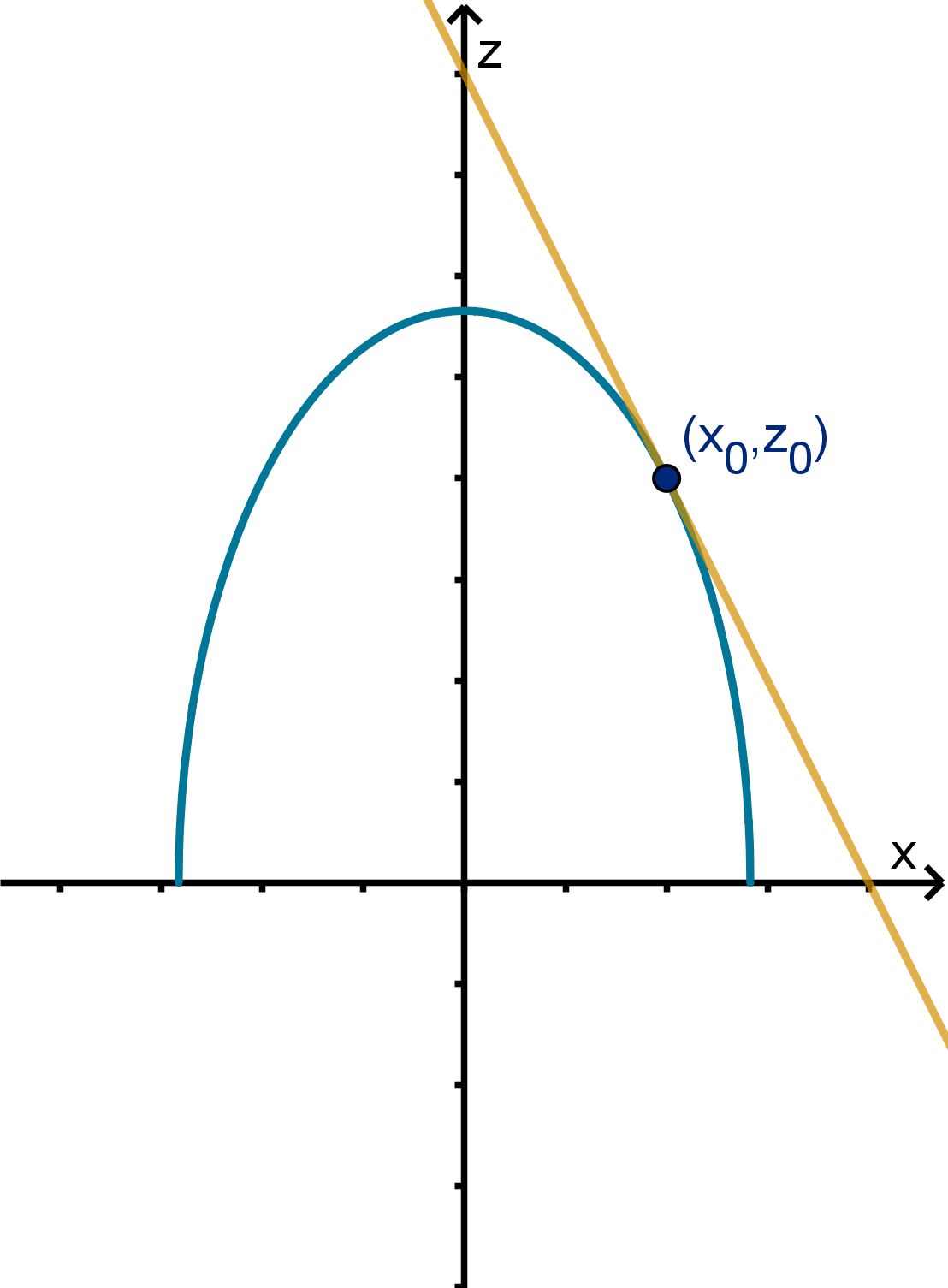
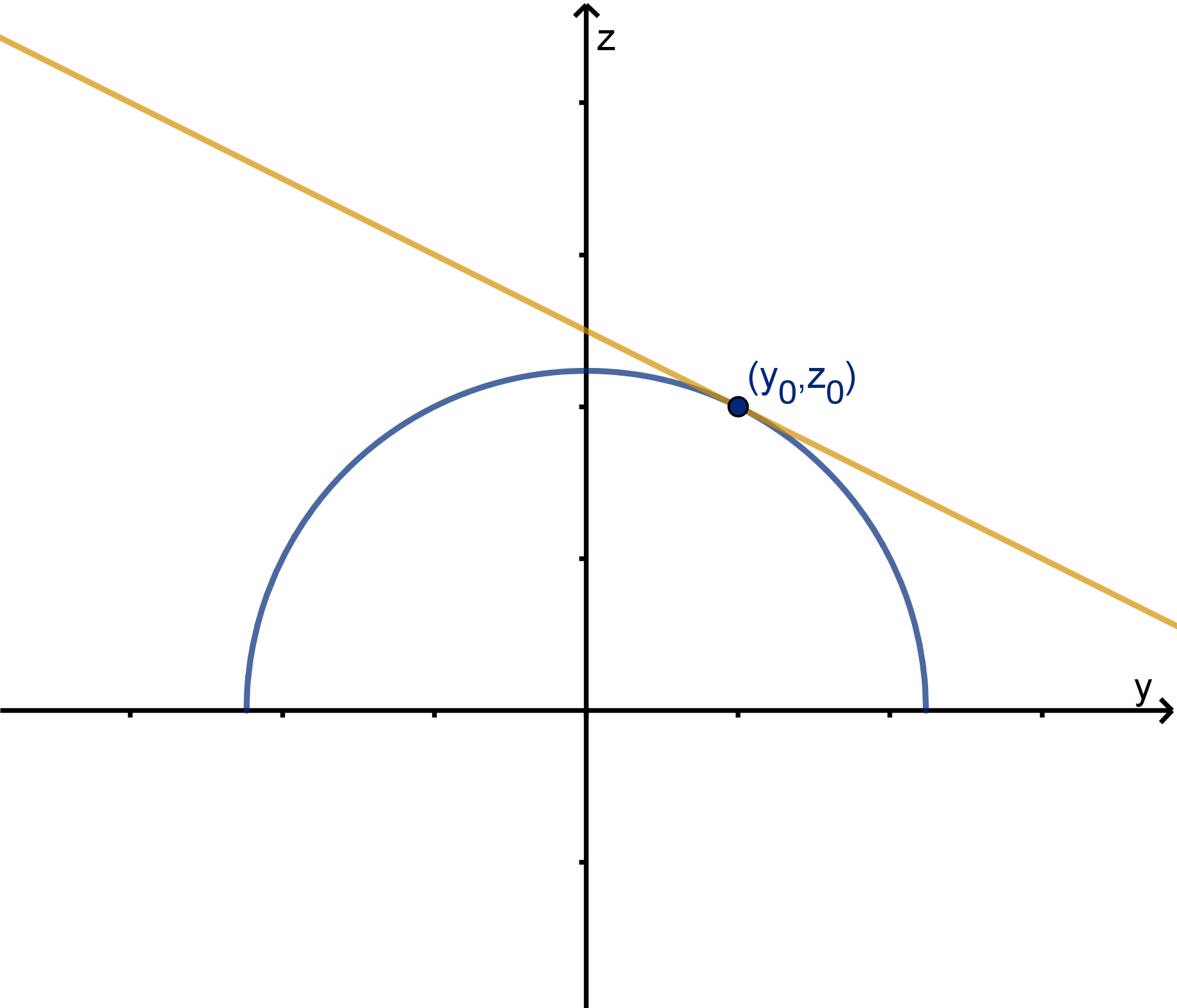
This shows that the tangent plane does contain these two tangent lines.
296
Example 4.5.2
Writing the Equation of a Tangent Plane
Give an equation of the tangent plane to f(x, y) =
√
xe
y
at (4, 0)
Solution
Writing the formula requires us to fill in 5 values.
1 x
0
= 4 is given.
2 y
0
= 0 is given.
3 z
0
is the height of the graph at (4, 0) which is
√
4e
0
= 2.
4 To compute f
x
(x
0
, y
0
) we compute the partial derivative function
f
x
(x, y) =
1
2
√
x
√
e
y
.
Then we evaluate at (4, 0).
f
x
(4, 0) =
1
2
√
4
√
e
0
=
1
4
.
5 f
y
(x
0
, y
0
) is similar though we will use the chain rule.
f
y
(x, y) =
√
x
1
2
√
e
y
e
y
f
y
(4, 0) =
√
4
1
2
√
e
0
e
0
= 1
We plug these values into the tangent plane formula.
z − 2 =
1
4
(x − 4) + 1(y −0)
which simplifies to
z − 2 =
1
4
(x − 4) + y.
297
Question 4.5.3
How Do We Rewrite a Tangent Plane as a Function?
Definition
If we write z as a function L(x, y), we obtain the linearization of f at (x
0
, y
0
).
L(x, y) = f(x
0
, y
0
) + f
x
(x
0
, y
0
)(x − x
0
) + f
y
(x
0
, y
0
)(y −y
0
)
If the graph z = f(x, y) has a tangent plane, then L(x, y) approximates the values of f near (x
0
, y
0
).
Notice f(x
0
, y
0
) just calculates the value of z
0
. This formula is equivalent to the tangent plane
equation after we solve for z by adding z
0
to both sides.
Example 4.5.4
Approximating a Function
Use a linearization to approximate the value of
√
4.02e
0.05
.
Solution
We don’t know
√
4.02e
0.05
, but we can think of this as the value of the function f(x, y) =
√
xe
y
. We
don’t know the value of this function at (4.02, 0.05), but the point (4, 0) is nearby, and we can evaluate
it there. This is where we’ll produce our linearization. We already produced the equation of the tangent
plane in Example .4.5.2.
z − 2 =
1
4
(x − 4) + y
We write z as the function L(x, y) and solve for it:
L(x, y) = 2 +
1
4
(x − 4) + y
For points near (4, 0), L(x, y) is close to f(x, y). This is the basis of our approximation.
√
4.02e
0.05
= f(4.02, 0.05) ≈ L(4.02, 0.05)
≈ 2 +
1
4
(4.02 − 4) + 0.05
≈ 2 + 0.005 + 0.05
≈ 2.055
298
Question 4.5.5
How Does Differential Notation Work in More Variables?
The one-variable differential is a shorthand way to express change in the linearization of a function.
The differential dx is an independent variable. It can take on any value. The differential dy depends on
both x
0
and dx.
dy = f
′
(x
0
)dx
Once we’ve chosen x
0
and dx, dy is the amount that the tangent line to y = f(x) at x
0
rises when we
increase x by dx.
Figure: The differentials dx and dy on the tangent line to y = f (x)
The differential dz measures the change in the linearization of f(x, y) given particular changes in the
inputs: dx and dy. It is a useful shorthand when one is estimating the error in an initial computation.
Definition
For z = f (x, y), the differential or total differential dz is a function of a point (x
0
, y
0
) and two
independent variables dx and dy.
dz = f
x
(x
0
, y
0
)dx + f
y
(x
0
, y
0
)dy
=
∂z
∂x
dx +
∂z
∂y
dy
Remark
The differential formula is just the tangent plane formula with
dz = z − z
0
dx = x − x
0
dy = y − y
0
.
An old trigonometry application is to measure the height of a pole by standing at some distance.
We then measure the angle θ of incline to the top, as well as the distance b to the base. The height is
h = b tan θ.
299
Question 4.5.5
How Does Differential Notation Work in More Variables?
a
If the distance to the base is 13m and the angle of incline is
π
6
, what is the height of the pole?
b
Human measurement is never perfect. If our measurement of b is off by at most 0.1m and our
measurement of θ is off by at most
π
120
, use a differential to approximate the maximum possible
error in our h.
Solution
a
The height is 13 tan
π
6
=
13
√
3
.
b
To compute the differential, we need to know the partial derivatives of h:
∂h
∂b
= tan θ
∂h
∂θ
= b sec
2
θ
∂h
∂b
(
13,
π
6
)
=
1
√
3
∂h
∂θ
(
13,
π
6
)
=
56
3
We can now compute the differential.
dh =
∂h
∂b
db +
∂h
∂θ
dθ
=
1
√
3
db +
56
3
dθ
dh is largest when db = 0.1 and dθ is
π
120
.
max dh =
1
√
3
(0.1) +
56
3
π
120
=
1
10
√
3
+
13π
90
300
Section 4.5
Exercises
Summary Questions
Q1
What do you need to compute in order to write the equation of a tangent plane to z = f(x, y)
at (x
0
, y
0
, z
0
)?
Q2
For what kinds of functions are linear approximations useful?
Q3
How are the tangent plane and the linearization related?
Q4
How is the differential defined for a two variable function? What does each variable in the formula
mean?
4.5.1
Q5
Let p(x, y) = 3x + 5y − 2.
a
What is the graph z = p(x, y)? What is the significance of 3, 5 and −2?
b
Give the equation of the tangent plane to z = p(x, y) at (1, 4, 21)
c
How is the tangent plane equation related to z = p(x, y)? Why does this make sense?
Q6
Olivia computes the tangent plane of z = x
2
+ y
2
at (4, 3, 25). Her answer is z − 25 =
2x(x − 4) + 2y(y − 3).
a
Is this the equation of a plane? Explain.
b
What does Olivia need to do to fix her answer?
Q7
If the equation of the tangent plane of z = f(x, y) does not have a y in it, does that mean that
y is a free variable of f? Explain.
Q8
Can our tangent plane formula ever give us a plane parallel to the xy-plane? The xz-plane? The
zy-plane? Explain.
301
Section 4.5
Exercises
4.5.2
Q9
Compute the equation of the tangent plane to z =
p
36 − 4x
2
− y
2
at (2, 2, 4).
Q10
Let g(x, y) =
3x
2
+4x−2
e
(y
3
)
. Write the equation of the tangent plane to z = g(x, y) at (0, 1).
Q11
Let f(x, y) =
p
y
x
. Write the equation of the tangent plane to z = f(x, y) at (4, 36, 3).
Q12
Let f(x, y) = ln(x
2
+ y). Write the equation of the tagent plane to z = f(x, y) at (e
3
, 0, 6).
4.5.3
Q13
Write a linearization of f(x, y) = ye
xy
at (3, 2).
Q14
Write a linearization of g(x, y) = e
x
2
+y
2
at (3, −4).
4.5.4
Q15
Suppose you want to approximate
√
5.5e
0.3
by hand. Would using the linearization of f (x, y) =
√
xe
y
at (5, 0) be a good strategy? Explain.
Q16
Show how to use an appropriate linearization to approximate
1
5.12
sin
31π
30
.
Q17
Let g(x, y) =
x
2
y
. Suppose you don’t remember how to divide decimals. Show how you can use
a linearization of g to approximate
3.97
2
1.05
.
Q18
Show how to use a linearization to approximate the value of
q
(4.02)
2
+
√
80.93 by hand.
302
4.5.5
Q19
Let f(x, y) =
y
x
2
+y
2
. Write the differential of f at (4, 3).
Q20
Let g(p, q) = p ln q. Write the differential of g at (3, e
2
).
Q21
Boris is measuring the area of a rectangular field, so he can decide how much grass seed to buy.
According to his measurements, the field is 30m by 50m, giving an area of 1500m
2
. If we accept
that each of his measurements has an error no larger than 0.2m, use a differential to approximate
the maximum error in his area computation.
Q22
Suppose I decide to invest $10, 000 expecting a 6% annual rate of return for 12 years, after which
I’ll use it to purchase a house. The formula for compound interest
P = P
0
e
rt
indicates that when I want to buy a house, I will have P = 10, 000e
0.72
.
I accept that my expected rate of return might have an error of up to dr = 2%. Also, I may
decide to buy a house up to dt = 3 years before or after I expected.
a
Write the formula for the differential dP at (r
0
, t
0
) = (0.06, 12).
b
Given my assumptions, what is the maximum estimated error dP in my initial calculation?
c
What is the actual maximum error in P ?
Q23
Let z = 2x −y
3
. At the point (x, y) = (5, 2), what is the maximum value of the differential dz?
Q24
Let f (x, y) be a function. What differential and what inputs into that differential would you use
to approximate f(5.5, 3.2) − f(4.7, 3.8).
Synthesis & Extension
Q25
Let L(x, y) be the linearization of f(x, y) at (3, 2). If f
yy
(x, y) < 0 for all (x, y), at which points
can we guarantee that L(x, y) either under or overestimates the value of f(x, y)? Explain.
Q26
Let f (x, y) = 25 − (x + 1)
2
− (y − 3)
2
. Describe the set of points (a, b) such that the tangent
plane to z = f (x, y) at (a, b, f(a, b)) passes through the origin.
303
Section 4.5
Exercises
Q27
Here is a table of selected values for a function f(x, y)
y
x
0 2 4 6 8 10
0 2 5 8 10 11 11
2 6 9 12 14 15 15
4 9 12 15 17 18 18
6 12 15 18 20 21 21
8 14 17 20 22 23 23
10 17 20 23 25 23 23
a
Using any reasonable approximation method, show how to produce a linearization of f(x, y)
at (4, 2).
b
Does your linearization over or underestimate f(10, 2)? Explain what that suggests about
one or more derivatives of f(x, y).
Q28 a
Give an equation of the plane that passes through the points (3, 4, 2), (5, 5, 1) and (6, 2, 6).
b
Suppose there is a function f(x, y) and the plane in part
a
is tangent to the graph z =
f(x, y) at (3, 4, 2). What partial derivatives of f can you compute exactly (be specific)?
Compute them.
304