For a straight line,
the slope can be obtained by drawing two points on the line \((x_1,y_1)\), \((x_2,y_2)\) and computing \(k=(y_2-y_1)/(x_2-x_1)\).
The slope of a line is constant, independent of which pair of points you choose.
Slope of \(f\) at \(x=a\) means the slope of its tangent line at \(x=a\).
\[\text{slope at } a = \lim_{x\to a} \frac{f(x)-f(a)}{x-a}\]
Remark. Unlike a line whose slope is constant, slopes of \(f\) at different points can be different (depending on what \(f\) is). That's why we specify the slope of \(f\) at a particular point (say, at \(x=a\)).
Example 1. Find the slope of the parabola \(y=x^2\) at \(x=1\).
Sol: Its slope at \(x=1\) is:
\[\lim_{x\to 1} \frac{f(x)-f(1)}{x-1} = \lim_{x\to 1}\frac{x^2-1}{x-1} = \lim_{x\to 1} (x+1)=2\]
(aka the derivative of \(f\) at \(x=1\))
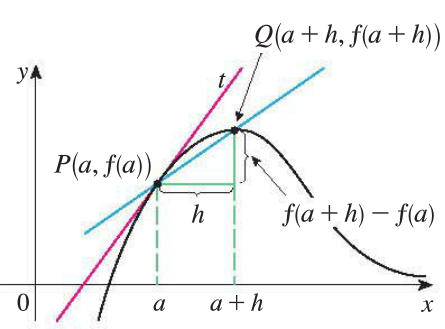
Write \(x=a+h\), hence \(x\to a\) is equivalent to \(h\to 0\). Then we have an equivalent definition \[\text{slope at } a = \lim_{h\to 0} \frac{f(a+h)-f(a)}{h}\]
Example 2. Compute the slope of \(y=\frac{1}{x}\) at \(x=2\) and find the tangent line at that point.
Sol:\[\lim_{h\to 0} \frac{f(2+h)-f(2)}{h}=
\lim_{h\to 0} \frac{\frac{1}{2+h}-\frac{1}{2}}{h}=\lim_{h\to 0} \frac{\frac{2-(2+h)}{2(2+h)}}{h} = \lim_{h\to 0}\frac{-1}{2(2+h)}=-\frac{1}{4}\]
The tangent line at \(x=2\) has slope \(-\frac{1}{4}\) and goes through \((2,\frac{1}{2})\).
So its equation is: \(y-\frac{1}{2}=-\frac{1}{4}(x-2)\)

Equation of motion: \(s=f(t)\), where \(f\) is called a position function
Average velocity over the time interval \([a,a+h]\): \[\text{average velocity over } [a,a+h]: \frac{f(a+h)-f(a)}{h}\]
Instantaneous velocity at \(t=a\) is the limit of the above average velocity as \(h\to 0\)
Instantaneous velocity at \(t=a\): \[\lim_{h\to 0} \frac{f(a+h)-f(a)}{h}\]
(aka the derivative of \(f\) at \(a\))
Example 3. If the location of a jogging snail on horizontal axis is \(f(t)=t^2\) as a function of time \(t\) (seconds). What is the velocity after \(1\) second?
Sol: same to Example 1.
The speed is defined as the absolute value of velocity.
The derivative of \(f\) at \(a\), denoted by \(f'(a)\), is given by \[f'(a)=\lim_{h\to 0} \frac{f(a+h)-f(a)}{h}\]
Example 4. If \(f(x)=x^2+3x\), find \(f'(1)\).
Sol:
\[
\begin{aligned}
\lim_{h\to 0} \frac{f(1+h)-f(1)}{h}&=
\lim_{h\to 0} \frac{[(1+h)^2+3(1+h)]-[1+3]}{h}\\
&=\lim_{h\to 0} \frac{h^2+5h}{h} = \lim_{h\to 0} (h+5)=5
\end{aligned}
\]
Ex. Let \(f(x)=\sqrt{x}\). For \(a>0\), find \(f'(a)\). (Hint: try to rationalize certain expression if you get stuck)
For \(y=f(x)\),
increment of \(x\) from \(x_1\) to \(x_2\): \(\Delta x = x_2-x_1\)
yields a change in \(y\), i.e.,
\(\Delta y=f(x_2)-f(x_1)\).
The difference quotient
\[\frac{\Delta y}{\Delta x}=\frac{f(x_2)-f(x_1)}{x_2-x_1}\]
yields the average rate of change of \(y\) over the interval \([x_1,x_2]\).
If \(x_2\to x_1\),
the (instantaneous) rate of change of \(y\) at \(x=x_1\) is given by
\[\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}=\lim_{x_2\to x_1}\frac{f(x_2)-f(x_1)}{x_2-x_1},\]
which is nothing but the derivative \(f'(x_1)\).
Large \(|f'(a)|\) ==> rapid/steep rate of change at \(a\); Small \(|f'(a)|\) ==> slow/flat rate of change at \(a\).