MATH 111 Calculus I \(\quad\;\;\) Instructor: Difeng Cai

2.2 The Limit of a Function

Infinite Limits

\(\lim_{x\to a}f(x)=\infty\) means that the values of \(f(x)\) can be made arbitrarily large by taking \(x\) sufficiently close to \(a\), but not equal to \(a\). ( \(f(x)\) "blows up" when \(x\) approaches \(a\) )

Since \(\infty\) is not a number, \(\lim_{x\to a}f(x)=\infty\) implies that the limit doest not exist when \(x\) tends to \(a\).

Similarly, \(\lim_{x\to a}f(x)=\infty\) means that \(f(x)\) can be arbitrarily large negative as \(x\) approaches \(a\).

Example. \(\lim_{x\to 0}\frac{1}{x^2}=\infty\) and \(\lim_{x\to 0}\frac{-1}{x^2}=-\infty\)

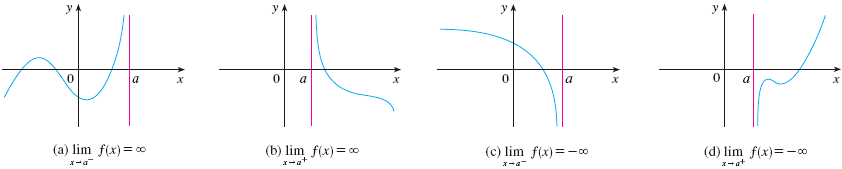
One-sided infinite limits can be defined similarly (see graphs below).

If \(f(x)\) tends to \(\infty\) or \(-\infty\) as \(x\) approaches \(a\) (either one-sided or two-sided), the vertical line \(x=a\) is called a vertical asymptote of \(y=f(x)\).

Ex. Find the limits.
(a). \(\lim_{x\to 4^-} \frac{5-x}{x-4}\) (b). \(\lim_{x\to 1^+}\ln(x^2-1)\) (c). \(\lim_{x\to (\frac{\pi}{2})^-} \tan x\) (d). \(\lim_{x\to (\frac{\pi}{2})^+} \tan x\)
Answer: (a).\(-\infty\) (b). \(-\infty\) (c).\(\infty\) (d).\(-\infty\)

2.3 Limit Laws

Assume \(\lim_{x\to a} f(x)\) exists. Then

• \(\lim_{x\to a} [f(x)]^n = \left[\lim_{x\to a} f(x)\right]^n\) (\(n\) is a positive integer)
• \(\lim_{x\to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x\to a} f(x)}\) (\(n\) is a positive integer; if \(n\) is even, we further assume \(\lim_{x\to a} f(x)>0\) because otherwise the limit does not exist)

Ex. (a). \(\lim_{x\to 1} \sqrt[3]{x^2-9}\) (b). \(\lim_{x\to -1} 3x-5x^2+1\)
Answer: (a). -2 (b). -7

Assume that the limits \(\lim_{x\to a} f(x)\) and \(\lim_{x\to a} g(x)\) exist. Then

• \[\lim_{x\to a} [ f(x)\pm g(x) ] = \lim_{x\to a} f(x) \pm \lim_{x\to a} g(x)\]
• \[\lim_{x\to a} [ f(x)g(x) ] = \lim_{x\to a} f(x) \cdot \lim_{x\to a} g(x)\]
• \[\lim_{x\to a} \frac{f(x)}{g(x)} = \frac{\lim_{x\to a} f(x)}{\lim_{x\to a} g(x)} \; \text{ if } \lim_{x\to a} g(x)\neq 0\]

What if \(\lim_{x\to a} g(x) =0\) ?

Compute \(\lim_{x\to a} \frac{f(x)}{g(x)}\) when \(\lim_{x\to a} g(x)=0\)

In this case, it is very likely that the expression can be simlified by canceling out common factors from the top and the bottom.

Example 1. \(\lim_{x\to 1} \frac{1-x^2}{x-1}\)
Solution: \(\lim_{x\to 1} x-1 = 0\) so we cannot apply the law above. Instead, we first simplify the expression: \[\frac{1-x^2}{x-1} = \frac{(1+x)(1-x)}{x-1} = -(1+x)\] Now it follows that \(\lim_{x\to 1} \frac{1-x^2}{x-1} = \lim_{x\to 1} -(1+x)=-2\).

Example 2. \(\lim_{x\to 0} \frac{(1-h)^2-1}{h}\)
Solution: Since \((1-h)^2-1=-2h+h^2\), we have \[\lim_{x\to 0} \frac{(1-h)^2-1}{h} = \lim_{x\to 0} \frac{-2h+h^2}{h}=\lim_{x\to 0} -2+h = -2\]

Example 3. \(\lim_{t\to 9} \frac{9-t}{3-\sqrt{t}}\)
Solution: \[\lim_{t\to 9} \frac{9-t}{3-\sqrt{t}}=\lim_{t\to 9} \frac{9-t}{3-\sqrt{t}} \frac{3+\sqrt{t}}{3+\sqrt{t}}=\lim_{t\to 9} \frac{(9-t)(3+\sqrt{t})}{9-t}=\lim_{t\to 9}3+\sqrt{t}=6\]

The Sandwich Theorem

Theorem 1. If \(f(x)\leq g(x)\) when \(x\) is near \(a\) (except possibly at \(a\)) and the limits of \(f\) and \(g\) both exist as \(x\) approaches \(a\), then \[\lim_{x\to a} f(x)\leq \lim_{x\to a}g(x)\]

Theorem 2(aka Sandwich Theorem or Squeeze Theorem) If \(f(x)\leq g(x)\leq h(x)\) when \(x\) is near \(a\) (except possibly at \(a\)) and \[\lim_{x\to a} f(x) = \lim_{x\to a}h(x) = L\] then \[\lim_{x\to a}g(x) = L\]

Ex. Show that \(\lim_{x\to 0}x^2\sin\frac{1}{x}=0\) using the Sandwich Theorem.