A function \(f\) is called a one-to-one function if it nevers takes on the same value twice; that is \[f(x_1)\neq f(x_2)\quad \text{whenever}\; x_1\neq x_2\]
Horizontal Line Test: A function is one-to-one if and only if no horizontal line intersects its graph more than once.
Examples. (a). \(f(x)=x^3\) is one-to-one; (b). \(f(x)=x^2\) is not one-to-one.
Given a one-to-one function \(y=f(x)\), its inverse function \(f^{-1}\) maps the output of \(f\) to the input: \[f^{-1}(y)=x\]
It follows from definition that:
Example. If \(y=f(x)=x^3+1\), then \(x=(y-1)^{1/3}=f^{-1}(y)\). Hence \(f^{-1}(x)=(x-1)^{1/3}\).
Steps to find the inverse of a one-to-one function
1. Write \(y=f(x)\)
2. Express \(x\) in terms of \(y\), written in the form of \(x=f^{-1}(y)\)
3. Interchange \(x\) and \(y\) to get \(y=f^{-1}(x)\)
Ex. The area of a disk of radius \(r\)(\(r\geq 0\)) is \(A(r) = \pi r^2\). Express \(r\) in terms of \(A\) and plot the graphs for functions \(A(r)\) and \(r(A)\).
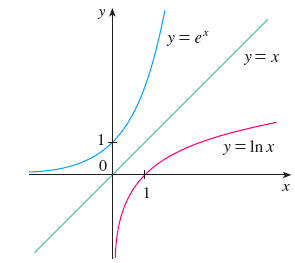
If \(y=b^x\) then \(x=\log_b b^x=\log_b y\) (where \(b>0\) and \(b\neq 1\) is a constant)
Logrithmic function(with base \(b\)): \(f(x)=\log_b x\) \(\;\) domain: \((0,\infty)\); range: \((-\infty,\infty)\)
Natural logarithm(i.e., base \(b=e\)): \(\log_e x = \ln x\)
Ex. Find \(x\) if \(\ln x =5\). (Answer: \(x=e^5\))
Ex. Solve the equation \(e^{1-x}=10\). (hint: apply \(\ln\) to both sides)
Examples. \(\log_2 8 = 3,\; \log_2 \frac{1}{8} = -3,\; \log_2 1 = 0, \; \log_2 \sqrt{2} = \frac{1}{2} \)
Example. If \(\log_b x = y\), then \(x=b^y\).

Example. \(\log_3 (3^5 \times 3^{1/2}) = \log_3 (3^{5.5}) = 5.5 = 5+1/2 = \log_3 (3^5) + \log_3(3^{1/2})\).
Thus \(\log_3 (3^5 \times 3^{1/2})= \log_3 (3^5) + \log_3(3^{1/2})\).
The above observation generalizes to the laws below for any positive numbers \(x,y\).
Ex. Evaluate \(\log_2 80 - \log_2 5\).
Answer: 4.
'\(\sin^{-1}\)' (or '\(\arcsin\)') is the inverse function of \(f(x)=\sin x\) (restricted to \(-\pi/2\leq x\leq \pi/2\)).
For \(\sin^{-1}(x)\) (or \(\arcsin^{-1}(x)\)), domain: \([-1,1]\) and range: \([-\pi/2,\pi/2]\).
Examples. \[\sin^{-1} \left(\frac{1}{2}\right) = \frac{\pi}{6},\quad \arcsin \left(\frac{-\sqrt{3}}{2}\right) = -\frac{\pi}{3},\quad \arcsin(-1)=-\pi/2\]
'\(\cos^{-1}\)' (or'\(\arccos\)') is the inverse function of \(f(x)=\cos x\) (restricted to \(0\leq x\leq \pi\)).
For \(\cos^{-1}(x)\) (or \(\arcsin^{-1}(x)\)), domain: \([-1,1]\) and range: \([0,\pi]\).
Examples. \[\cos^{-1} 0 = \frac{\pi}{2},\; \cos^{-1} \left(\frac{-1}{2}\right) = \frac{2\pi}{3}\]
'\(\tan^{-1}\)' (or '\(\arctan\)') is the inverse function of \(f(x)=\tan x\) (\(-\pi/2< x< \pi/2\)).
Domain: \((-\infty,\infty)\); range: \((-\pi/2,\pi/2)\)
Example. If \(\theta\in (-\pi/2,\pi/2)\), then \(\arctan\left(\tan\theta\right) = \theta\). \[\arctan\left(\frac{1}{\sqrt{3}}\right)=\frac{\pi}{6},\; \arctan 1 = \frac{\pi}{4}\]