MATH 111 Calculus I \(\quad\;\;\) Instructor: Difeng Cai
3.9 Related Rates
- Read the problem, identify and sketch the GEOMETRY.
- Set up an equation to connect quantities of interest. Depending on the geometry, for solids like cylinder/sphere/box, the equation could be the volume formula; for right-angled triangle/rectangle, the equation could be the area, the Pythagorean theorem \(x^2+y^2=z^2\), or trigs if angle is of interest.
- Differentiate (Chain Rule is often needed) both sides of the equation with respect to \(t\) and obtain an equation between the unknown rate and the given quantities
- Figure out and plug in the known quantities and solve for the unknown rate.
Example 1.
A cylindrical tank with radius \(5\) \(m\) is being filled with water at a rate of \(2\) \(m^3/min\). How fast is the height of the water increasing?
Sol:
- Geometry: cylinder; Quantities: volume of water(cylinder): \(V,\;\) height of water: \(h,\;\) radius of cylinder: \(r=5\) \(m,\;\) time: \(t\).
- Find an equation to relate \(V\) and \(h\): \[V = \text{area of base} \times\text{height} = \pi r^2 h = 25\pi h\]
- Differentiate w.r.t. \(t\): \[\dfrac{dV}{dt}=25\pi \dfrac{dh}{dt}\]
- Given: \(\dfrac{dV}{dt}=2\) \(m^3/min\quad\)
Unknown: \(\dfrac{dh}{dt}\)
- Plug in known rate and solve for the unknown rate: \[\dfrac{dh}{dt} = \frac{1}{25\pi}\dfrac{dV}{dt}=\frac{1}{25\pi}\cdot 2=\frac{2}{25\pi} \;m/min\]
Example 2.
The radius of a sphere is increasing at a rate of \(4 \; mm/s\). How fast is the volume increasing when the diameter is \(40 \; mm\)?
Sol:
- Geometry: sphere; Quantities: radius \(r,\;\) volume of a sphere \(V,\;\) time \(t\)
- Find an equation to relate \(V\) and \(r\): \[V = \frac{4}{3}\pi r^3\]
- Differentiate w.r.t. \(t\) (chain rule is needed for \(r^3\)): \[\dfrac{dV}{dt}=\frac{4}{3}\pi \dfrac{d}{dt}(r^3) = \frac{4}{3}\pi \cdot 3r^2 \dfrac{dr}{dt} = 4\pi r^2\dfrac{dr}{dt}\]
- Given: \(\dfrac{dr}{dt}=4 \; mm/s\quad\) Need to find: \(\dfrac{dV}{dt}\) when \(r=\frac{40}{2}=20\)
- Plug in known values and solve for the unknown rate: \[\dfrac{dV}{dt}=4\pi \left(\frac{40}{2}\right)^2\cdot 4=6400\pi \; mm^3/s\]
Example 3.
Two cars start moving from the same point. One travels south at \(60\) mi/h and the other travels west at \(25\) mi/h. At what rate is the distance between the cars increasing two hours later?
Sol:
- Geometry: right-angled triangle; Quantities: distance traveled by first car: \(x,\;\) distance traveled by second car: \(y,\;\) distance between two cars \(z\)
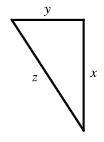
- Find an equation to relate \(x,y,z\): \[z^2 = x^2+y^2\]
- Differentiate w.r.t. \(t\): \[2z\cdot \dfrac{dz}{dt} = 2x\cdot \dfrac{dx}{dt} + 2y\cdot \dfrac{dy}{dt}\]
- Need to find: \(\dfrac{dz}{dt}\) two hours later (i.e., \(t=2\))
- Given: speed of first car: \(\dfrac{dx}{dt}=60,\;\) speed of second car: \(\dfrac{dy}{dt}=25\)
- Values of \(x,y,z\) ?
Two hours later, \(x=60\cdot 2=120\), \(y=25\cdot 2=50\), \(z=\sqrt{x^2+y^2}=\sqrt{120^2+50^2}=130\)
- Plug in known values and solve for the unknown rate \(\dfrac{dz}{dt}\):
\[ \dfrac{dz}{dt} = \frac{x}{z}\cdot \dfrac{dx}{dt} + \frac{y}{z}\cdot \dfrac{dy}{dt}\quad \text{according to the equation in 3.}\]
so \[\dfrac{dz}{dt}= \frac{120}{130}\cdot 60+\frac{50}{130}\cdot 25=\frac{8450}{130}=65 \; mi/h\]
"You have now completed the Master It."

