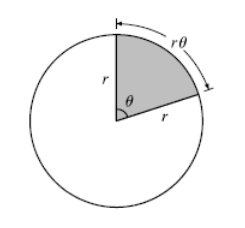
If you are offered one slice from a round pizza (in other words, a sector of a circle) and the slice must have a perimeter of 24 inches, what diameter pizza will reward you with the largest slice?
Sol:

Step 1. Understand what is optimized: largest slice of a pizza ==> maximal area of a sector
Step 2. Define variables: radius \(r\) and angle \(\theta\), and set up the object function: \[A = \dfrac{1}{2}r^2\theta\]
Step 3.
Find the constraint and express \(A\) as a function of one variable by eliminating "redundant" variables.
The perimeter must satisfy
\[2r+r\theta = 24\]
Thus \(\theta=(24-2r)/r\),
and we have
\[A(r)=\dfrac{1}{2}r^2(24-2r)/r=\dfrac{1}{2}r(24-2r)=-r^2+12r\]
The domain of \(A(r)\) is:
\[0 < r < 12\]
Step 4. Find the max or min of object function(in this case, max).
(1). Compute critical point of \(A(r)\)
\[A'(r)=-2r+12=0\; \to\; r=6\]
(2). Check the sign of \(A'(r)\) to see where \(A\) increases or decreases:
\(A'(r)>0\) if \(r<6\) and \(A'(r)<0\) if \(r>6\).
So as \(r\) goes from \(0\) to \(12\), \(A(r)\) first increases until \(r=6\) and then decreases.
Thus \(r=6\) yields the global maximum value \(A(6)=-6^2+12\times 6=36.\)
The diameter is \(2r=12\).