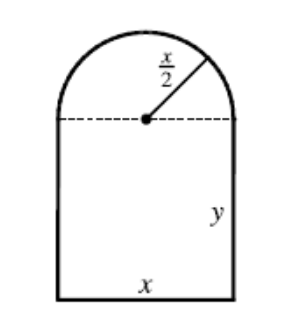
Example 1. The window you see in MSC entrance is a Norman window, which has the shape of a rectangle surmounted by a semicircle. (Thus the diameter of the semicircle is equal to the width of the rectangle.) If the perimeter of the window is 12 ft, find the value of width so that the greatest possible amount of light is admitted.
Sol:
Step 1. Understand what is optimized:
greatest amount of light ==> maximize the area of the window
Step 2. Set up the object function: let \(x\) denote the width of the ractangle and \(y\) the height of the rectangle,
\[A = \text{area of semicircle} + \text{area of rectangle} = \frac{1}{2}\pi\left(\frac{x}{2}\right)^2+xy\]
Step 3.
Write down the constraint, and then
express \(A\) as a function of one variable by eliminating "redundant" variables (don't forget to specify the domain of the function):
The constraint is
\[\text{perimeter} = \pi\frac{x}{2}+x+2y = 12,\quad x\geq 0, \; y\geq 0,\]
and thus
\[y = \frac{1}{2}\left[12-\left(\frac{\pi}{2}+1\right)x\right].\]
Insert this in the expression of area \(A\), we have:
\[A(x) = \frac{1}{2}\pi\left(\frac{x}{2}\right)^2+x \frac{1}{2}\left[12-\left(\frac{\pi}{2}+1\right)x\right] = \frac{-\pi-4}{8}x^2+6x.\]
The domain is: \(0\leq x \leq \frac{24}{\pi+2}\) according to the perimeter constraint (set \(y=0\) in the perimeter gives the largest value allowed for \(x\)).
Step 4.
Find the global max or min of object function(in this case, max):
\[A'(x)=\frac{-\pi-4}{4}x+6=0\quad \Rightarrow\quad x=\frac{24}{\pi+4}.\]
Is the critical point in the domain?
\[0<\frac{24}{\pi+4}<\frac{24}{\pi+2}\]
Yes, it's in the domain.
Is the critical point a global maximum ?
We see that \(A'(x)>0\) when \(x<\frac{24}{\pi+4}\) and \(A'(x)<0\) when \(x>\frac{24}{\pi+4}\).
Hence \(A(x)\) increases on \((0,\frac{24}{\pi+4})\)
and decreases on \((\frac{24}{\pi+4},\frac{24}{\pi+2})\).
The global max is achieved at \(x=\frac{24}{\pi+4}\).
Step 4. Another way to determine global max: To find the global max, it suffices to check values of \(A\) at critical point \(x=\frac{24}{\pi+4}\) and at endpoints of the domain and pick up the largest one. However, a possible drawback is that the value may not be easy to compute. For example, in this problem, you may encounter difficulty computing/simplifying the value at endpoint, \(A(\frac{24}{\pi+2})\) .
Example 2.
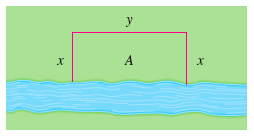
A farmer has 1000 ft of fencing and wants to fence off a rectangular field that borders a straight river. He needs no fence along the river. What are the dimensions of the field that has the largest area?
Sol:
Step 1. Understand what is optimized:
largest area ==> maximize the area \(A\)
Step 2. Set up the object function:
\(A = xy\), where \(x\) is the vertical length and \(y\) is the horizontal length (see figure in the bottom).
Step 3.
Express \(A\) as a function of one variable by eliminating "redundant" variables and write down the domain of the function:
\(2x+y=1000\), so
\[A(x)=x(1000-2x)=1000x-2x^2,\quad 0\leq x\leq 1000.\]
Step 4. Find the max or min of object function(in this case, max):
\[A'(x)=1000-4x=0\quad\text{implies}\quad x=250.\]
\[A''(x) = -4 < 0\;\;\text{for all}\;\; x\]
so the graph of \(A\) is always concave downward, and \(A(250)\) is the max. (second derivative test)
The dimensions should be \(x=250, y=1000-2x=500\) and the largest area is
\[A(250)=250(1000-2\times250)=250\times500=125000.\]