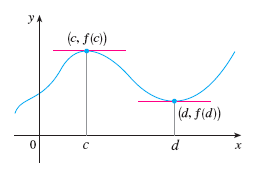
Fermat's Theorem:
If \(f\) has local max or min at \(c\), and if \(f'(c)\) exists, then \(f'(c)=0.\)
The converse is not true.
ATTENTION: \(f'(c)=0\) does not mean \(f(c)\) is a local max or min.
Counter example. \(f(x)=x^3\). \(f'(0)=0\) but \(f\) has no max or min (local or global).
Example of Fermat's Theorem. \(f(x)=\sin x\) has a local max at \(x=\frac{\pi}{2}\) and \(f'(\frac{\pi}{2})=0\).
A critical number of a function is a number in the domain of \(f\) such that either \(f'(c)=0\) or \(f'(c)\) does not exist.
Example 1. Find the critical numbers of \(f(x)=6x^3-9x^2-36x.\)
Sol: Solving \(f'(x)=0\) yields \(x=-1\) and \(x=2\). So \(-1, 2\) are critical numbers.
Example 2. Find the critical numbers of \(f(x)=\sqrt{x}.\)
Sol: Domain of \(f\): \(x\geq 0\).
Derivative is \(f'(x)=\frac{1}{2}x^{-1/2}\).
Note that \(f'(x)\neq 0\) for \(x>0\) and \(f'(0)\) does not exist.
Hence the only critical number is \(0\).
(Comment: this is an example where \(0\) is in the domain of \(f\) and \(f'(0)\) does not exist)
The Closed Interval Method for finding global max & min of continuous \(f\) over \([a,b]\):
1. Find values of \(f\) at endpoints of the interval: \(f(a)\), \(f(b)\)
2. Find values of \(f\) at all critical points: first find all critical points, then evaluate \(f\) at those pts
3. Choose the largest from Steps 1,2 as max and the smallest as min
Example. Find the global max and min of
\[f(x)=x^3-3x^2+1, \quad -\frac{1}{2}\leq x\leq 4\]
Sol:
Step 1. Find values of \(f\) at endpoints:
| endpts | \(f\) values |
|---|---|
| \(\frac{1}{2}\) | \(\frac{1}{8}\) |
| \(4\) | \(17\) |
Step 2. Find all critical pts and values of \(f\) at those pts. Since \(f'(x)\) exists for all \(x\), all critical pts are roots of
\[f'(x)=3x^2-6x=0.\]
Hence the critical numbers are \(x=0\) and \(x=2\).
Values of \(f\) at critical pts are
| critical pts | \(f\) values |
|---|---|
| \(0\) | \(1\) |
| \(2\) | \(-3\) |
Step 3. Candidates of extreme values are \(\frac{1}{8}, 17, 1, -3\). We see that: max = \(17\), min = \(-3\).
Example. Find where the function
\(f(x)=3x^4-4x^3-12x^2+5\) is increasing or decreasing.
Sol:
\[f'(x)=12x^3-12x^2-24x=12x(x-2)(x+1).\]
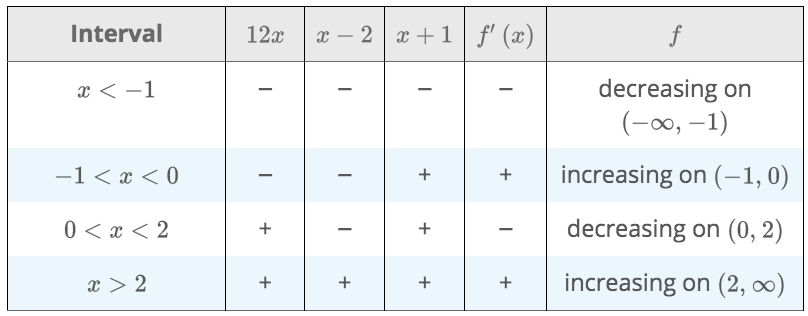
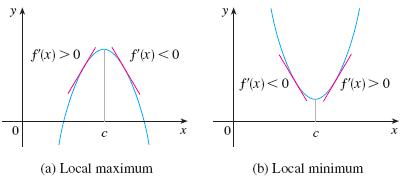
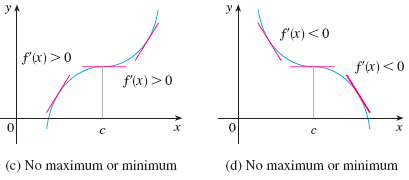
Ex. Find the local max and min of \(f(x)=3x^4-4x^3-12x^2+5\).
concave upward (CU) and
concave downward (CD)
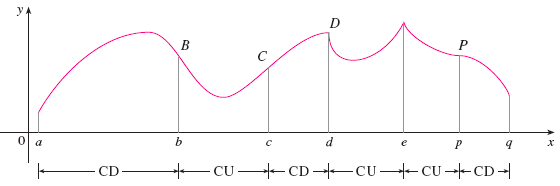
If \(f''(c)=0\), then \(c\) is called an inflection point
Example. \(f''\) is continuous near \(c\). \(f'(1)=0\) and \(f''(1)=-1\). What can you say about \(f\) at \(x=1\) ?
Sol: \(f(1)\) is a local maximum.
Ex. Discuss the curve \(y=x^3\) in terms of monotonicity, concavity, inflection point, max/min, etc.