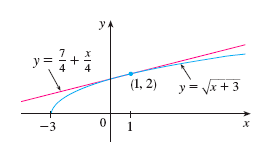
Example.
Use the linearization of \(f(x)=\sqrt{x+3}\) at \(a=1\) to approximate the number \(\sqrt{4.05}\).
Sol:
The linearization of \(f(x)=\sqrt{x+3}\) at \(a=1\) (aka "the tangent line") is
\[L(x)=\frac{1}{4}(x-1)+2=\frac{x}{4}+\frac{7}{4}.\]
Then
\[\sqrt{4.05}=\sqrt{1.05+3}=f(1.05)\approx L(1.05)=\frac{1}{4}(1.05-1)+2=2.0125.\]
The exact value is \(\sqrt{4.05}\approx 2.01246\dots\) What can we say about our estimate (without knowing the exact value)?
The approximations are overestimates because the tangent line lies above the curve (see figure below).

Ex. Find the linearization of \(f(x)=\frac{1}{x+2}\) at \(a=1\) and use it to estimate the value of \(\frac{1}{2.91}\).
Sol: Linearization: \(L(x)=-\frac{1}{9}(x-1)+\frac{1}{3}\).
\[\frac{1}{2.91}=f(0.91)\approx L(0.91)=
-\frac{1}{9}(0.91-1)+\frac{1}{3}
= -\frac{1}{9}(-0.09)+\frac{1}{3}=
0.01+\frac{1}{3}\approx 0.343333\]
\(f(c)\) is the global(absolute) maximum value of \(f\) on \(D\) if \(f(c)\geq f(x)\) for all \(x\in D\).
\(f(c)\) is the global(absolute) minimum value of \(f\) on \(D\) if \(f(c)\leq f(x)\) for all \(x\in D\).
Global max & min are called extreme values of \(f\).
\(f(c)\) is the local maximum value of \(f\) if \(f(c)\geq f(x)\) when \(x\) is near \(c\).
\(f(c)\) is the local minimum value of \(f\) if \(f(c)\leq f(x)\) when \(x\) is near \(c\).
ATTENTION. According to the textbook, if \(c\) is an endpoint, then \(f(c)\) cannot be a local max or min
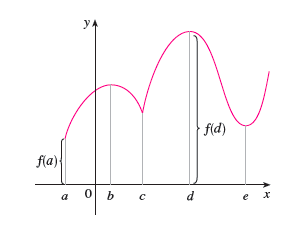
Example 1. \(f\) is shown below. \(f(a)\) is the global maximum, \(f(b)\) is a local maximum, \(f(c)\) is a local minimum, \(f(d)\) is both a local maximum and the global maximum, \(f(e)\) is a local minimum.
Example 2. If \(f(x)=x^2\), then \(f(0)=0\) is the global minimum. \(f\) has no maximum value.
Ex.
Sketch the graph of \(f(x)=\sin x\),
where \(0\leq x < \frac{\pi}{2}\).
Find the following:
(1). global max (2). global min (3). local max (4). local min
Sol: (1). DNE (2). 0 (3). DNE (4). DNE
Continuous on closed interval ==> both global max and min exist
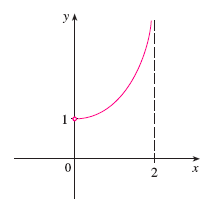
Example 1.
\(f\) has global min \(f(2)=0\) but no global max.
Note that \(3\) is not a global max of \(f\) because it cannot be attained by any \(f(c)\) with \(c\) in \([0,2]\).
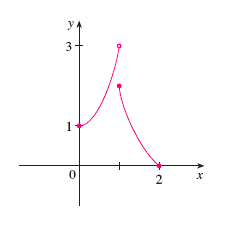
Example 2.
\(f\) has neither a max nor a min.
Both \(f(0)\) and \(f(2)\) are undefined
since the domain of \(f\) is \((0,2)\).