MATH 111 Calculus I \(\quad\;\;\) Instructor: Difeng Cai

TEST REVIEW

Hot Topics

• exponential functions, logarithmic functions
• limits, asymptotes, continuity, discontinuity
• derivatives, tangent lines

Derivatives, Tangent Lines

0. Definition of \(f'(x)\) as a limit of different quotient

\[f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\]

Use limit to calculate the derivative of a given function. See day10.

1. How to find the tangent line of \(f\) at \(x=x_0\) ?

Recall that a line can be determined by specifying its slope, say \(k\), and a point \((x_0,y_0)\) on it.
The point-slope form is: \(y-y_0=k(x-x_0)\).
For a given funciton \(f\), the slope of the tangent line at \(x=x_0\) is equal to \(f'(x_0)\). The point \((x_0,f(x_0))\) is on the tangent line. Hence the equation of the tangent line at \(x_0\) is \[y-f(x_0)=f'(x_0)(x-x_0),\] or equivalently, \[y=f'(x_0)(x-x_0)+f(x_0).\]

Ex. Find the tangent line of \(f(x)=(x-1)^2\) at \(x=2\).
Key: \(y=2(x-2)+1=2x-3\).
(When calculating derivative using limit definition, it's much easier to use \(a^2-b^2=(a+b)(a-b)\) instead of expanding the square terms)

2. Sketch graph of \(f'\) given graph of \(f\)

Tips:

1. Check where does \(f\) have a horizontal tangent line. If \(f\) has a horizontal tangent at \(x=a\), then \(f'(a)=0\).
2. Find the intervals on which \(f\) is increasing(going up), then \(f'>0\) over those intervals. Rapid increase ==> \(f'\) is a large positive number
3. Find the intervals on which \(f\) is decreasing(going down), then \(f'<0\) over those intervals. Rapid decrease ==> \(f'\) is a large negative number

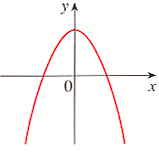
Example. Consider the graph of \(f\) given below. What does the graph of \(f'\) look like?

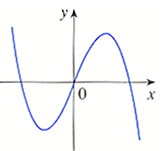
Starting from the left, \(f\) first decreases, then increases, then decreases again. So we deduce that \(f'\) is first negative, then positive, in the end negative again. The zeros of \(f'\) are where \(f\) has a horizontal tangent line. See below for a sketch of \(f'\).

3. Cases where \(f\) is not differentiable at \(x=a\)

See day11.

Limits, Asymptotes, Continuity, Discontinuity

1. Compute \(\lim\limits_{x\to a}f(x)\) given formula of \(f\)

Cases. \[\frac{0}{0},\quad \frac{\infty}{\infty},\quad\text{others}\]

• \(\frac{0}{0}\) example (cancelation trick): \(\lim\limits_{x\to 2} \frac{x-2}{x^2-3x+2}=\lim\limits_{x\to 2} \frac{x-2}{(x-2)(x-1)}=\lim\limits_{x\to 2} \frac{1}{x-1}=1\)
• \(\frac{\infty}{\infty}\) example (leading term trick): \(\lim\limits_{x\to \infty} \frac{3x-2}{x^2-x+1}=\lim\limits_{x\to \infty} \frac{3x}{x^2} = \lim\limits_{x\to \infty} \frac{3}{x}=0\)
• others(no trick): \(\lim\limits_{x\to -\infty} \frac{3}{x-1}=0\), \(\lim\limits_{x\to -\infty} \frac{e^x-1}{e^x+1} = \frac{0-1}{0+1}=-1\)

2. Find \(\lim\limits_{x\to a} f(x)\) based on its graph

See Quiz 3.

3. Horizontal Asymptotes

\(f(x)\) has a horizontal asymptote \(y=y_0\) if \(\lim\limits_{x\to \infty}f(x)=y_0\) or \(\lim\limits_{x\to -\infty}f(x)=y_0\)

For horizontal asymptote, be sure to check both \(x\to \infty\) and \(x\to -\infty\) to find all possible asymptotes.

Examples.
(a). \(f(x)=\frac{1}{x}+9\) has one one horizontal asymptote \(y=9\)
(b). \(f(x)=\frac{3x^2-1}{x^2+2x}\) has one horizontal asymptote \(y=3\) as \(\lim\limits_{x\to \infty}f(x)=\lim\limits_{x\to -\infty}f(x)=3\)

4. Types of discontinuities

See day8: http://www.math.emory.edu/~dcai7/teaching.html

Exponential Functions, Logarithmic Functions

Properties of exponential functions

• If \(a>1\), then \(\lim\limits_{x\to -\infty} a^x=0\) and \(\lim\limits_{x\to \infty} a^x=\infty\).
• If \(0<a<1\), then \(\lim\limits_{x\to -\infty} a^x=\infty\) and \(\lim\limits_{x\to \infty} a^x=0\).
• Because \(\lim\limits_{x\to -\infty} 2^x=0\), \(f(x)=2^x\) has a horizontal asymptote \(y=0\).

Properties of logarithmic functions

Domain of \(f(x)=\ln x\) is \((0,\infty)\), range is \((-\infty,\infty)\) \[\ln \left(e^s\right) = s\] \[\ln a +\ln b = \ln (ab)\] \[\ln a -\ln b = \ln (\frac{a}{b})\]

Modelling with exponential functions

For more info about \(\exp, \log\), see Quiz 2, day3, day5: http://www.math.emory.edu/~dcai7/teaching.html

Domain, Range, Graph of a Function

See Quiz 1, Quiz 2