Joint Analysis of X-ray Ptychography and X-ray Fluorescence Reconstruction

This project was completed by Mingke Tian and Eric Zou under the mentorship of Yuanzhe Xi as part of the 2025 Emory REU program.

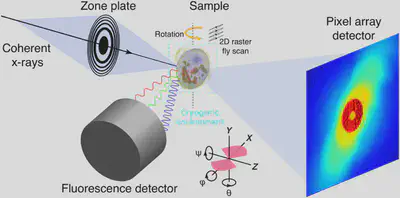
Ptychographic Reconstruction Part

In the traditional way, we use separate methods for ptychographic and fluorescence reconstruction. We consider a ptychography experiment where the observed data $d_i$ is modeled as:

$$ d_i = \vert\mathcal{F}(\mathbf{P}_i \mathbf{z})\vert^2 + \epsilon_i $$

where:

• $\mathcal{F}$: 2D discrete Fourier transform operator
• $\mathbf{P}_i$: Probe matrix
• $z_i$: the object itself which can be written as $z = x + y_i$

Reconstruction Problem

The reconstruction loss function is formulated as the following:

$$ \min_{\mathbf{P},\mathbf{z}} \Phi(\mathbf{P},\mathbf{z}) = \frac{1}{2} \sum_{j=1}^{N} \Vert \vert \mathcal{F}(\mathbf{P}_j \mathbf{z})\vert - \sqrt{d_j} \Vert_2^2 $$

X-ray Fluorescence Reconstruction

X-ray fluorescence reconstruct the real part of the image $x$ using a deconvolution method:

$$ \min_{\mathbf{w},\mathbf{P}} \sum_{e=1}^{N_e} \Vert \vert\mathbf{P}\vert^2 * \mathbf{w}_e - D_e \Vert_2^2 $$

where $\mathbf{w}$ represents elemental concentration maps. $D_e$ corresponds to the experimental flourescence map of element $e$.

Separate Optimization Framework

Separate optimization of ptychographic and fluorescence reconstruction may lead to the results:

$$ \min_{\mathbf{P},\mathbf{z}} \Phi(\mathbf{P},\mathbf{z}) + \min_{\mathbf{w},\mathbf{P}} \sum_{e=1}^{N_e} \Vert \vert\mathbf{P}\vert^2 * \mathbf{w}_e - D_e \Vert_2^2 $$

where $\alpha$ is a scaling parameter balancing between the two objectives.

Joint Optimization Framework

We propose a simultaneous optimization approach:

$$ \min_{\mathbf{w},\mathbf{P},\mathbf{z}} \sum_{e=1}^{N_e} \Vert \vert\mathbf{P}\vert^2 * \mathbf{w}_e - D_e \Vert_2^2 + \alpha \sum_{j=1}^{N} \Vert \vert \mathcal{F}(\mathbf{P}_j (\sum_e \mathbf{w}_e + i \beta))\vert - \sqrt{d_j} \Vert_2^2 $$

By using joint method, the loss function is consistently less than the original loss function from the separate method.

Absorption Coefficient Connection

The absorption coefficient relates to elemental concentrations via:

$$ \mathbf{z} = \delta + i \beta, \quad \delta = \sum_e \mathbf{w}_e \mu_e $$

Conclusion

This joint framework aims to enhance both ptychographic and fluorescence data processing, leveraging their complementarity for improved reconstruction.

Reference

[1] Deng, J., Vine, D.J., Chen, S. et al. X-ray ptychographic and fluorescence microscopy of frozen-hydrated cells using continuous scanning. Sci Rep 7, 445 (2017). https://doi.org/10.1038/s41598-017-00569-y